0 446280 446288 446294 446298 446304 446306 446310 446316 446318 446324 446330 446334 446336 446340 446346 446348 446354 446358 446360 446364 446366 446370 446372 446374 446375 446376 446378 446379 446380 446382 446384 446388 446390 446394 446396 446400 446406 446408 446414 446418 446420 446424 446430 446436 446438 446444 446448 446450 446456 446460 446466 446474 447348
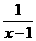 ,x∈(1,2)
,x∈(1,2)  ,则arg
,则arg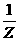 是
是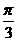 B.
B.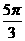 C.
C.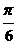 ?D.
?D.
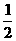 ) ?B.(0,
) ?B.(0,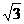 ,则这个圆锥的全面积是
,则这个圆锥的全面积是 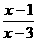 >0的解集为
>0的解集为 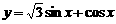
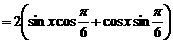
 ,
, 。
--3分
。
--3分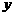 取得最大值必须且只需
取得最大值必须且只需 ,
,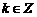 ,
,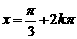 ,
, 的集合为
的集合为 。
--6分
。
--6分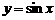 的图象向左平移
的图象向左平移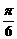 ,得到函数
,得到函数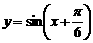 的图象;
--9分
的图象;
--9分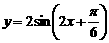 的图象;
的图象;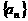 的公差为
的公差为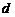 ,则
,则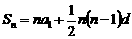
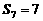 ,
,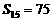 ,
,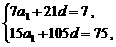 --6分
--6分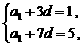
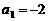 ,
, 。
--8分
。
--8分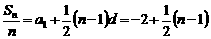 ,
,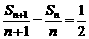 ,
, 是等差数列,其首项为
是等差数列,其首项为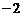 ,公差为
,公差为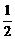 ,
, 。
--12分
。
--12分 (I)证明:连结
(I)证明:连结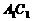 、AC,AC和BD交于O,连结
、AC,AC和BD交于O,连结 。
。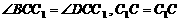 ,
, ,
, ,
,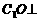 BD,
--3分
BD,
--3分 。
。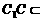 平面
平面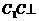 BD。
--6分
BD。
--6分 时,能使
时,能使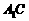 ⊥平面
⊥平面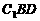 。
。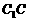 ,
,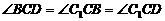 ,
, ∶GO=2∶1。
∶GO=2∶1。 平面
平面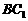 ⊥
⊥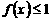 即
即 ,
,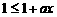 ,即
,即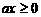 ,其中常数
,其中常数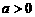 。
。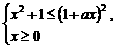
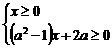 --3分
--3分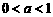 时,所给不等式的解集为
时,所给不等式的解集为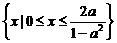 ;
;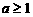 时,所给不等式的解集为
时,所给不等式的解集为 。 --6分
。 --6分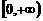 上任取
上任取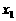 ,
, ,使得
,使得
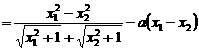
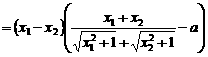 。 --9分
。 --9分 ,且
,且 ,
, ,
,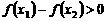 ,
,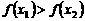 。
。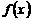 在区间
在区间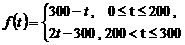 --2分
--2分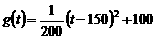 ,
, 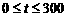 --4分
--4分 时刻的纯收益为
时刻的纯收益为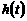 ,则由题意得
,则由题意得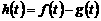 ,
, --6分
--6分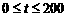 时,配方整理得
时,配方整理得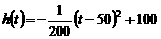 ,
,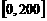 上的最大值100;
上的最大值100;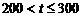 时,配方整理得
时,配方整理得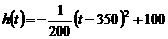 ,
,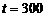 时,
时,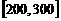 上的最大值87.5;--10分
上的最大值87.5;--10分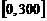 上可以取最大值100,此时,
上可以取最大值100,此时, 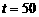 ,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
,即从二月一日开始的第50天时,上市的西红柿纯收益最大。 ,则CD⊥
,则CD⊥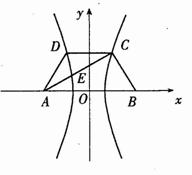 依题意,记A
依题意,记A ,B
,B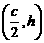 ,C
,C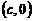 ,其中
,其中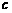 为双曲线的半焦距,
为双曲线的半焦距,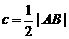 ,
,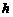 是梯形的高。
是梯形的高。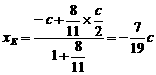 ,
,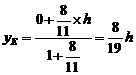 。
--5分
。
--5分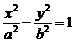 ,则离心率
,则离心率 。
。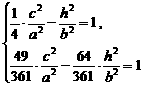 --10分
--10分
 ,代入②得
,代入②得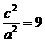 。
。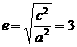 。
--14分
。
--14分 (15)
(15)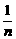 (16)②③
(16)②③