3.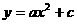 和
和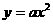 ,通过解析式我们得知,对于同一个自变量
,通过解析式我们得知,对于同一个自变量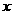 的值,
的值,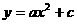 的值总比
的值总比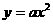 的值大或小|
的值大或小|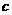 |个单位.(如
|个单位.(如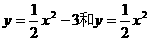 .对于每一个
.对于每一个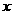 的值,
的值,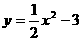 的值总比
的值总比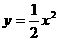 的值小于3个单位.而
的值小于3个单位.而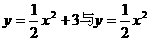 ,对于同一个
,对于同一个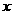 的值
的值
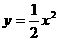 的值大3个单位)这一特点反映在函数图象上就是将
的值大3个单位)这一特点反映在函数图象上就是将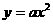 的图象上的各点向上平移|
的图象上的各点向上平移|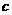 |个单位.(
|个单位.(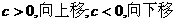 )此时
)此时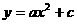 的对称轴仍是
的对称轴仍是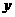 轴,而顶点坐标是(0,
轴,而顶点坐标是(0,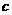 ),它的开口方向与
),它的开口方向与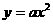 的图象的开口一样,
的图象的开口一样,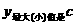 ;而
;而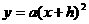 的图象与
的图象与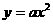 的图象各点具有对于同一个
的图象各点具有对于同一个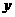 值,
值,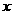 值不同,譬如
值不同,譬如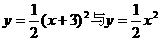 列表:
列表:
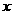 |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
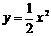 |
… |
|
|
|
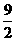 |
2 |
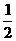 |
0 |
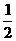 |
2 |
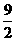 |
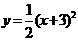 |
… |
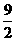 |
2 |
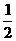 |
0 |
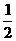 |
2 |
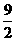 |
|
|
|
对于同一个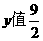 ,在
,在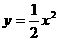 中,
中,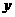 对应的
对应的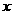 是-3和3,在
是-3和3,在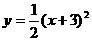 中,
中, 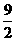 对应的
对应的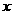 值是-6和0.而-6比-3小3个单位,0比3小3个单位,这说明:对于同一个
值是-6和0.而-6比-3小3个单位,0比3小3个单位,这说明:对于同一个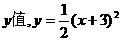 所对应的
所对应的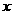 值,总比
值,总比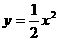 所对应的
所对应的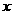 值小3个单位.
值小3个单位.
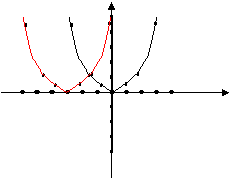 y
y
x
这些特性反映在图象上就是将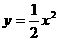 图象上各点向左平移3个单位得到函数
图象上各点向左平移3个单位得到函数 的图象上的点,函数
的图象上的点,函数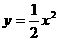 的图象整个向左平移3个单位得到
的图象整个向左平移3个单位得到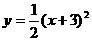 的图象.同理,将
的图象.同理,将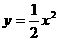 的图象向右平移2个单位得到
的图象向右平移2个单位得到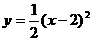 的图象,总之将
的图象,总之将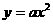 的图象向左或向右平移|h|个单位(h>0时向左移动;h<0时,向右移)就得到
的图象向左或向右平移|h|个单位(h>0时向左移动;h<0时,向右移)就得到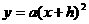 的图象,由于图象左右移动,对称轴发生变化,不是
的图象,由于图象左右移动,对称轴发生变化,不是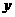 轴了,而是直线
轴了,而是直线 ,顶点是(
,顶点是(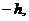 0).
0).
由于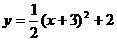 的图象是将
的图象是将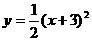 的图象向上平移2个单位,而
的图象向上平移2个单位,而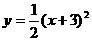 是由
是由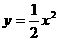 的图象向左平移3个单位,所以
的图象向左平移3个单位,所以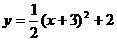 是由
是由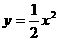 的图象向左平移3个单位,再向上平移2个单位得到的,其顶点是(-3,2),对称轴是
的图象向左平移3个单位,再向上平移2个单位得到的,其顶点是(-3,2),对称轴是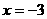 .
.
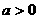 时,抛物线的开口向上;
时,抛物线的开口向上;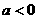 时,抛物线的开口向下;对称轴是
时,抛物线的开口向下;对称轴是 =0;
=0;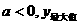 =0.
=0.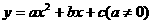 叫做二次函数.
叫做二次函数.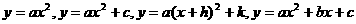 的图象的位置关系.
的图象的位置关系.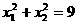
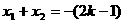
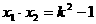 得
得
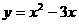 与
与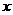 轴交于A(0,0)和B(3,0)
轴交于A(0,0)和B(3,0)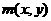
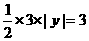
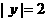
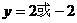
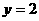 舍去(若
舍去(若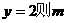 点必在
点必在 是钝角三角形,与△A
是钝角三角形,与△A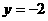 时,
时, 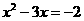
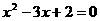
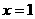
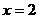
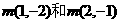
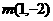 也会在[因为
也会在[因为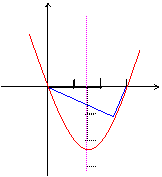 y
y 
 2.
2.  3.
3. 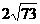 4. 30° 5.
4. 30° 5. 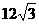 6. (9,0),(0,-3)
6. (9,0),(0,-3) 
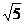 8.
8.  9. ¨5或3 10. (3,-2) 11.
9. ¨5或3 10. (3,-2) 11. 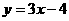
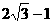 13. 4 14.
13. 4 14. 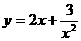 15.
15.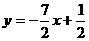
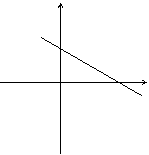 提示:设
提示:设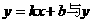 轴交于(0,2)
y
轴交于(0,2)
y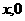 ),则S△AOB=
),则S△AOB=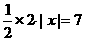 A(0,2)
A(0,2)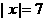
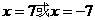
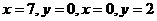 代入公式
代入公式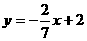 ,
,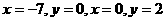 代入得
代入得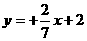
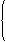
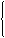 交点C的坐标是
交点C的坐标是 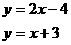 的解
的解 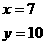 S△ABC=25 S△CPQ=
S△ABC=25 S△CPQ=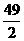
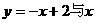 轴交于(2,0),
轴交于(2,0),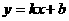 与
与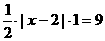
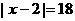
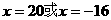
 ∴
∴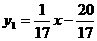 和
和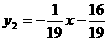 y
y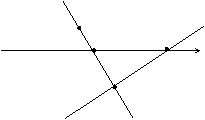
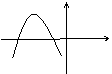 二次函数
二次函数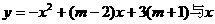 轴交于A(
轴交于A(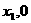 )和B(
)和B(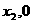 ),
),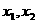 是
是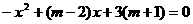 的根.线段OA的长是
的根.线段OA的长是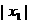 ,线段OB的长是
,线段OB的长是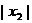 ,由题意得:
,由题意得: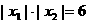 ,若图象是
,若图象是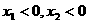
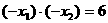
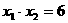 两根之积是6
两根之积是6 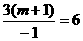
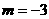
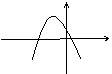 若图象是
若图象是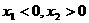

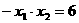
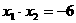
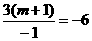
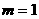
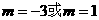 S△ABC=3或15
S△ABC=3或15