摘要：理解并掌握二次函数的概念.
网址：http://m.1010jiajiao.com/timu3_id_445354[举报]
如图，二次函数y=ax2-（a+1）x（a为常数，且0＜a＜1）的图象过原点O并与x轴交于点P；过点A（1，-1）的直线l垂直y轴于点B，并与二次函数的图象交于点Q，以OA为直径的⊙C交x轴于点D，连接DQ．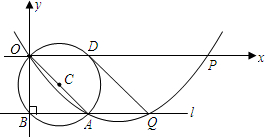
（1）点B与⊙C的位置关系是 ；
（2）点A是否在二次函数的图象上 ；（填“是”或“否”）
（3）若DQ恰好为⊙C的切线，
①猜想：四边形OAQD的形状是 ，证明你的猜想；
②求二次函数的表达式． 查看习题详情和答案>>
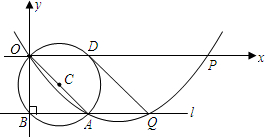
（1）点B与⊙C的位置关系是
（2）点A是否在二次函数的图象上
（3）若DQ恰好为⊙C的切线，
①猜想：四边形OAQD的形状是
②求二次函数的表达式． 查看习题详情和答案>>
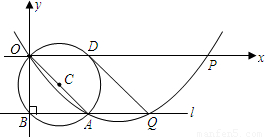
如图，二次函数y=ax2-（a+1）x（a为常数，且0＜a＜1）的图象过原点O并与x轴交于点P；过点A（1，-1）的直线l垂直y轴于点B，并与二次函数的图象交于点Q，以OA为直径的⊙C交x轴于点D，连接DQ．
（1）点B与⊙C的位置关系是______；
（2）点A是否在二次函数的图象上______；（填“是”或“否”）
（3）若DQ恰好为⊙C的切线，
①猜想：四边形OAQD的形状是______，证明你的猜想；
②求二次函数的表达式．
查看习题详情和答案>>
（1）点B与⊙C的位置关系是______；
（2）点A是否在二次函数的图象上______；（填“是”或“否”）
（3）若DQ恰好为⊙C的切线，
①猜想：四边形OAQD的形状是______，证明你的猜想；
②求二次函数的表达式．
查看习题详情和答案>>
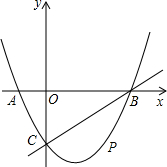如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点．
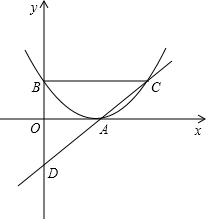AB=2，又关于x的方程x2-（b+2ac）x+m=0（m＜0）的两个实数根互为相反数．