摘要：了解二次函数的图象的位置关系.

网址：http://m.1010jiajiao.com/timu3_id_445355[举报]

（2012•白下区一模）（1）在学习《二次函数的图象和性质》时，我们从“数”和“形”两个方面对二次函数y=x²和y=（x+3）²进行了研究，现在让我们重温这一过程．
①填表（表中阴影部分不需填空）：

②从对应点的位置看，函数y=x²的图象与函数y=（x+3）²的图象的位置有什么关系？
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向

（填“左”或“右”）平移

个单位长度可以得到函数y=2x+6的图象．
②直接写出函数y=

（k、m是常数，k≠0，m＞0）的两条不同类型的性质．

查看习题详情和答案>>

（1）在学习《二次函数的图象和性质》时，我们从“数”和“形”两个方面对二次函数y=x²和y=（x+3）²进行了研究，现在让我们重温这一过程．
①填表（表中阴影部分不需填空）：

②从对应点的位置看，函数y=x²的图象与函数y=（x+3）²的图象的位置有什么关系？
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向______（填“左”或“右”）平移______个单位长度可以得到函数y=2x+6的图象．
②直接写出函数y=

（k、m是常数，k≠0，m＞0）的两条不同类型的性质．
查看习题详情和答案>>

（1）在学习《二次函数的图象和性质》时，我们从“数”和“形”两个方面对二次函数y=x²和y=（x+3）²进行了研究，现在让我们重温这一过程．
①填表（表中阴影部分不需填空）：

②从对应点的位置看，函数y=x²的图象与函数y=（x+3）²的图象的位置有什么关系？
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向______（填“左”或“右”）平移______个单位长度可以得到函数y=2x+6的图象．
②直接写出函数y=

（k、m是常数，k≠0，m＞0）的两条不同类型的性质．
查看习题详情和答案>>

（1）在学习《二次函数的图象和性质》时，我们从“数”和“形”两个方面对二次函数y=x²和y=（x+3）²进行了研究，现在让我们重温这一过程．
①填表（表中阴影部分不需填空）：
x … -6 -5 -4 -3 -2 -1 0 1 2 3 …
y=x² … ▲ ▲ ▲ ▲ ▲ ▲ ▲ …
y=（x+3）² … ▲ ▲ ▲ ▲ ▲ ▲ ▲ …
②从对应点的位置看，函数y=x²的图象与函数y=（x+3）²的图象的位置有什么关系？
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向（填“左”或“右”）平移个单位长度可以得到函数y=2x+6的图象．
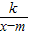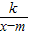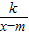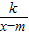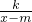②直接写出函数y= $数学公式$ （k、m是常数，k≠0，m＞0）的两条不同类型的性质．

查看习题详情和答案>>