0 139233 139241 139247 139251 139257 139259 139263 139269 139271 139277 139283 139287 139289 139293 139299 139301 139307 139311 139313 139317 139319 139323 139325 139327 139328 139329 139331 139332 139333 139335 139337 139341 139343 139347 139349 139353 139359 139361 139367 139371 139373 139377 139383 139389 139391 139397 139401 139403 139409 139413 139419 139427 447348
 . (2011昌平二模)等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点.则
. (2011昌平二模)等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点.则 如图所示的区域中,左边为垂直纸面向里的匀强磁场,磁感应强度为 B ,右边是一个电场强度大小未知的匀强电场,其方向平行于OC且垂直于磁场方向.一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中,初速度方向与边界线的夹角θ=600
,粒子恰好从C孔垂直于OC射入匀强电场,最后打在Q点,已知OQ= 2 OC ,
如图所示的区域中,左边为垂直纸面向里的匀强磁场,磁感应强度为 B ,右边是一个电场强度大小未知的匀强电场,其方向平行于OC且垂直于磁场方向.一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中,初速度方向与边界线的夹角θ=600
,粒子恰好从C孔垂直于OC射入匀强电场,最后打在Q点,已知OQ= 2 OC , (1)画出粒子运动的轨迹如图示的三分之一圆弧
(1)画出粒子运动的轨迹如图示的三分之一圆弧 ……………………2分
……………………2分 ……………………1分
……………………1分 …………………………………………1分
…………………………………………1分 …………………………1分
…………………………1分 场中类平抛运动
场中类平抛运动 ……1分
……1分
 ……1分
……1分  …………………1分
…………………1分 …………2分 解得粒子到达Q点时的动能为
…………2分 解得粒子到达Q点时的动能为 ……1
……1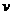 的某种带电粒子,带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍.已知该带电粒子的质量为
的某种带电粒子,带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍.已知该带电粒子的质量为 、电荷量为
、电荷量为 ,不考虑带电粒子的重力.
,不考虑带电粒子的重力.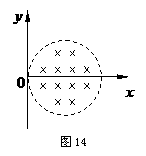 (1)推导带电粒子在磁场空间做圆周运动的轨道半径;
(1)推导带电粒子在磁场空间做圆周运动的轨道半径;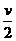 ,求该粒子第一次回到O点经历的时间.
,求该粒子第一次回到O点经历的时间.
 ………………………………………………………………………2分
………………………………………………………………………2分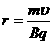 ……………………………………………………………………………1分
……………………………………………………………………………1分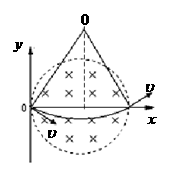 (2)设粒子飞出和进入磁场的速度方向夹角为
(2)设粒子飞出和进入磁场的速度方向夹角为 ,则
,则 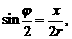 x是粒子在磁场中轨迹的两端点的直线距离.
x是粒子在磁场中轨迹的两端点的直线距离.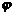 最大值.且2R=r
最大值.且2R=r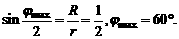 …………………3分(3)当粒子的速度减小为
…………………3分(3)当粒子的速度减小为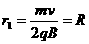 ………………………………………………………1分
………………………………………………………1分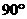 时与边界相撞弹回,由对称性知粒子经过四个这样的过程后第一次回到O点,亦即经历时间为一个周期.……………1分
时与边界相撞弹回,由对称性知粒子经过四个这样的过程后第一次回到O点,亦即经历时间为一个周期.……………1分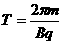 .
.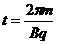 …………………………………………………………………………1分
…………………………………………………………………………1分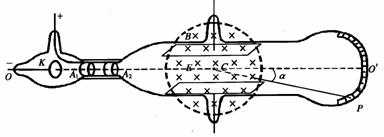

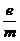 ;
;


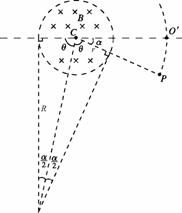
 。同样可求出电子的比荷
。同样可求出电子的比荷
 eE=evB
①
…………(2分)
eE=evB
①
…………(2分)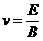 ②
…………(2分)
②
…………(2分)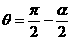 ③
…………(1分)
③
…………(1分)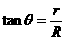 ④
…………(1分)
④
…………(1分) 又因:
又因: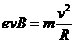 ⑤
…………(1分)
⑤
…………(1分)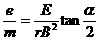 ⑥
…………(1分)
⑥
…………(1分) 有
有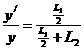 ⑦
…………(1分)
⑦
…………(1分)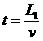

 ⑧
⑧ 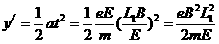 ⑨ …………(1分)
⑨ …………(1分)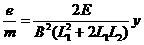 …………(1分)
…………(1分)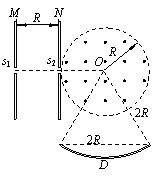 (11分)如图所示,相距为R的两块平行金属板M、N正对着放置,s1、s2分别为M、N板上的小孔,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R。以O为圆心、R为半径的圆形区域内存在磁感应强度为B、方向垂直纸面向外的匀强磁场。D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板。质量为m、带电量为+q的粒子,经s1进入M、N间的电场后,通过s2进入磁场。粒子在s1处的速度和粒子所受的重力均不计。
(11分)如图所示,相距为R的两块平行金属板M、N正对着放置,s1、s2分别为M、N板上的小孔,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R。以O为圆心、R为半径的圆形区域内存在磁感应强度为B、方向垂直纸面向外的匀强磁场。D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板。质量为m、带电量为+q的粒子,经s1进入M、N间的电场后,通过s2进入磁场。粒子在s1处的速度和粒子所受的重力均不计。 达s2的过程中,根据动能定理得
达s2的过程中,根据动能定理得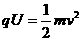 ①
[1分]
①
[1分]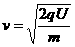 [1分]
[1分]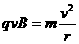 ②
[1分]
②
[1分]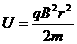
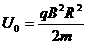 [1分]
[1分]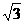 R
[1分]
R
[1分]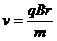
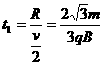 [1分]
[1分]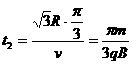 [1分]
[1分]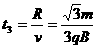 [1分]
[1分]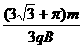 [1分]
[1分] (12分)如图所示,某空间内存在着正交的匀强电场和匀强磁场,电场方向水平向右,磁场方向垂直于纸面向里。一段光滑绝缘的圆弧轨道AC固定在场中,圆弧所在平面与电场平行,圆弧的圆心为O,半径R=1.8m,连线OA在竖直方向上,圆弧所对应的圆心角
(12分)如图所示,某空间内存在着正交的匀强电场和匀强磁场,电场方向水平向右,磁场方向垂直于纸面向里。一段光滑绝缘的圆弧轨道AC固定在场中,圆弧所在平面与电场平行,圆弧的圆心为O,半径R=1.8m,连线OA在竖直方向上,圆弧所对应的圆心角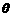 =37°。现有一质量m=3.6×10-4kg、电荷量q=9.0×10-4C的
=37°。现有一质量m=3.6×10-4kg、电荷量q=9.0×10-4C的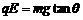
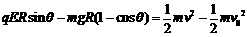 ②
②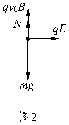 解得
v=5.0m/s
③
解得
v=5.0m/s
③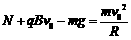 ④
④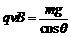 ⑤
⑤ 如图所示,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ
如图所示,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ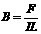 可知,B与F成正比,与IL成反比
可知,B与F成正比,与IL成反比 ②.E和B都沿水平方向,并与电子运动方向相反
②.E和B都沿水平方向,并与电子运动方向相反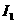 时,小磁针偏转了
时,小磁针偏转了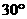 ;当通过导线电流为
;当通过导线电流为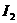 时,小磁针偏转了
时,小磁针偏转了 ,则下列说法中正确的是( )
,则下列说法中正确的是( )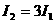 B.
B.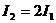 C.
C.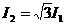 D.无法确定
D.无法确定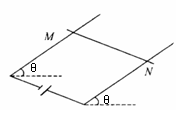 .(2011房山期末)如图所示,在匀强磁场B的区域内有一光滑倾斜金属导轨,倾角为θ,导轨间距为L,在其上垂直导轨放置一根质量为m的导线,接以如图所示的电源,电流强度为I,通电导线恰好静止,则匀强磁场的磁感强度必须满足一定条件,下述所给条件正确的是.
.(2011房山期末)如图所示,在匀强磁场B的区域内有一光滑倾斜金属导轨,倾角为θ,导轨间距为L,在其上垂直导轨放置一根质量为m的导线,接以如图所示的电源,电流强度为I,通电导线恰好静止,则匀强磁场的磁感强度必须满足一定条件,下述所给条件正确的是.