0 136616 136624 136630 136634 136640 136642 136646 136652 136654 136660 136666 136670 136672 136676 136682 136684 136690 136694 136696 136700 136702 136706 136708 136710 136711 136712 136714 136715 136716 136718 136720 136724 136726 136730 136732 136736 136742 136744 136750 136754 136756 136760 136766 136772 136774 136780 136784 136786 136792 136796 136802 136810 447348
 如图所示,在水平地面上固定一倾角θ=37°、表面光滑的斜面体,物体A以v1=6m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中。(A、B均可看作质点, sin37°=0.6,cos37°=0.8,g取10m/s2)求:
如图所示,在水平地面上固定一倾角θ=37°、表面光滑的斜面体,物体A以v1=6m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中。(A、B均可看作质点, sin37°=0.6,cos37°=0.8,g取10m/s2)求: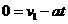
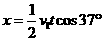 =2.4m(2分)
=2.4m(2分)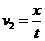 =2.4m/s(2分)
=2.4m/s(2分)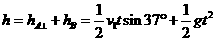 =6.8m(4分)
=6.8m(4分)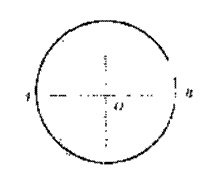 如图所示,半径为R的光滑圆轨道竖直放置,长为2R的轻质杆两端各固定一个可视为质点的小球A、B,把轻杆水平放入圆形轨道内,若m,2m,m0,m,重力加速度为g,现由静止释放两球,当轻杆到达竖直位置时,求:
如图所示,半径为R的光滑圆轨道竖直放置,长为2R的轻质杆两端各固定一个可视为质点的小球A、B,把轻杆水平放入圆形轨道内,若m,2m,m0,m,重力加速度为g,现由静止释放两球,当轻杆到达竖直位置时,求: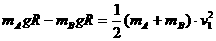 …………(2分)
…………(2分)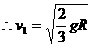 (1分)
(1分)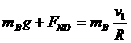 (1分)
(1分) ………………(1分)
………………(1分)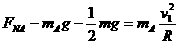 (1分)
(1分)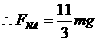 (1分)
(1分)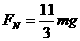 (1分)
(1分)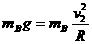 (1分)
(1分)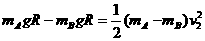
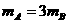
 如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细线的下端吊一个质量为m的铁球(可视作质点),球离地的高度h=L,当绳受到大小为3mg的拉力时就会断裂.现让环与球一起以
如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细线的下端吊一个质量为m的铁球(可视作质点),球离地的高度h=L,当绳受到大小为3mg的拉力时就会断裂.现让环与球一起以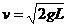 的速度向右运动,在A处环被挡住而立即停止,A离右墙的水平距离也为L.不计空气阻力,已知当地的重力加速度为
的速度向右运动,在A处环被挡住而立即停止,A离右墙的水平距离也为L.不计空气阻力,已知当地的重力加速度为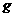 .试求:
.试求: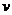 绕A点做圆周运动,根据牛顿第二定律和圆周运动的向心力公式有:
绕A点做圆周运动,根据牛顿第二定律和圆周运动的向心力公式有: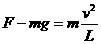 .............2分
.............2分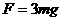 ...............................1分
...............................1分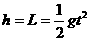 .........................1分
.........................1分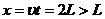 .....................................1分
.....................................1分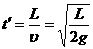 .....................1分
.....................1分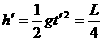 .............................1分
.............................1分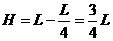 ...............1分
...............1分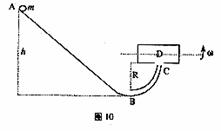 如图10所示,质量为m可看作质点的小球从静止开始沿斜面由A点滑到B点后,进入与斜面圆滑连接的
如图10所示,质量为m可看作质点的小球从静止开始沿斜面由A点滑到B点后,进入与斜面圆滑连接的 竖直圆弧管道
竖直圆弧管道 ,管道出口为C,圆弧半径R=15cm,AB的竖直高度差h=35cm. 在紧靠出口C处,有一水平放置且绕其水平轴线匀速旋转的圆筒(不计筒皮厚度),筒上开有小孔D,筒旋转时,小孔D恰好能经过出口C处. 若小球射出C口时,恰好能接着穿过D孔,并且还能再从D孔向上穿出圆筒,小球返回后又先后两次向下穿过D孔而未发生碰撞. 不计摩擦和空气阻力,取g=10m/s2,问:
,管道出口为C,圆弧半径R=15cm,AB的竖直高度差h=35cm. 在紧靠出口C处,有一水平放置且绕其水平轴线匀速旋转的圆筒(不计筒皮厚度),筒上开有小孔D,筒旋转时,小孔D恰好能经过出口C处. 若小球射出C口时,恰好能接着穿过D孔,并且还能再从D孔向上穿出圆筒,小球返回后又先后两次向下穿过D孔而未发生碰撞. 不计摩擦和空气阻力,取g=10m/s2,问: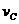 为多少?
为多少?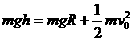 ① …………2分
① …………2分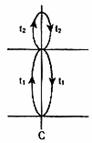
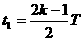 (k=1,2,3……) ② ……2分
(k=1,2,3……) ② ……2分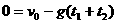 ④ …………2分
④ …………2分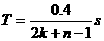 ⑤ …………1分
⑤ …………1分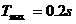 …………1分
…………1分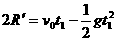 ⑥ …………2分
⑥ …………2分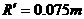 …………1分
…………1分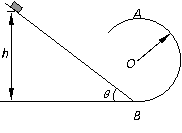
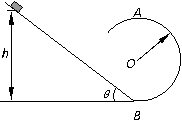 解:(1)物块沿斜面下滑过程中,在重力、支持力和摩擦力作用下做匀加速运动,设下滑加速度为a ,到达斜面底端B时的速度为v,则
解:(1)物块沿斜面下滑过程中,在重力、支持力和摩擦力作用下做匀加速运动,设下滑加速度为a ,到达斜面底端B时的速度为v,则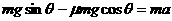 (2分)
(2分)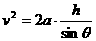 (2分)
(2分) 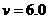 m/s (2分)
m/s (2分)
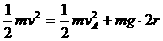 (2分)
(2分)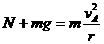 (2分)
(2分)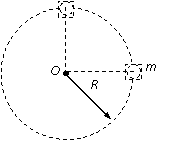 则该盒子做匀速圆周运动的周期为多少?
则该盒子做匀速圆周运动的周期为多少?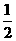 做匀速圆周运动,
做匀速圆周运动,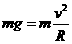 (1分)
(1分) 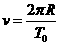 (1分)
(1分)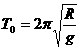 (2分)
(2分)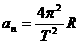 (1分)
(1分)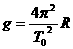 且
且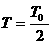 (1分)
(1分)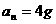 (1分)
(1分)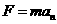 (2分)
(2分)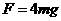 (1分)
(1分)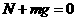 (2分)
(2分)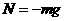 (1分)
(1分) (1)当圆盘的角速度多大时,滑块从圆盘上滑落?
(1)当圆盘的角速度多大时,滑块从圆盘上滑落?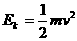 = μmgr=0.1J------------------------------------③
= μmgr=0.1J------------------------------------③ 如图所示,将一根光滑的细金属棒折成V形,顶角为2
如图所示,将一根光滑的细金属棒折成V形,顶角为2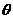 ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,
,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,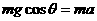 ① (2分)
① (2分)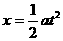 ② (2分)
② (2分)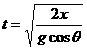 ③ (1分)
③ (1分)
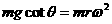 ④ (2分)
④ (2分)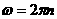 ⑤ (2分)
⑤ (2分)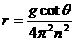 ⑥ (1分)
⑥ (1分)