网址:http://m.1010jiajiao.com/timu3_id_1356534[举报]
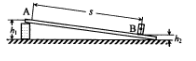
某同学为了探究物体在斜面上运动时摩擦力与斜面倾角的关系,设计实验装置如图。长直平板一端放在水平桌面上,另一端架在一物块上。在平板上标出A、B两点,B点处放置一光电门,用光电计时器记录滑块通过光电门时挡光的时间。
实验步骤如下:
①用游标卡尺测量滑块的挡光长度d,用天平测量滑块的质量m;
②用直尺测量AB之间的距离s,A点到水平桌面的垂直距离![]() ,B点到水平桌面的垂直距离
,B点到水平桌面的垂直距离![]() ;
;
③将滑块从A点静止释放,由光电计时器读出滑块的挡光时间t;
④重复步骤③数次,并求挡光时间的平均值![]() ;
;
⑤利用所测数据求出摩擦力![]() 和斜面倾角的余弦值
和斜面倾角的余弦值![]() ;
;
⑥多次改变斜面的倾角,重复实验步骤②③④⑤,做出![]() 关系曲线。
关系曲线。
⑴用测量的物理量完成下列各式(重力加速度为g):
①斜面倾角的余弦![]() = ;
= ;
②滑块通过光电门时的速度v= ;
③滑块运动时的加速度a= ;
④滑块运动时所受到的摩擦阻力f= ;
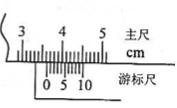
(2)测量滑块挡光长度的游标卡尺读数如图所示,读得d= 。
查看习题详情和答案>>如果悬挂物F的重力越来越大时,小车的加速度会无限制地增加吗?
简要回答: .
(DIS是数字化信息系统的简称)
 查看习题详情和答案>>
查看习题详情和答案>>
利用如图1所示装置探究动能定理,在斜面体的斜面上,一质量为1kg的物块后面固定一条通过打点计时器的纸带。先打点,然后让物块从静止开始沿斜面匀加速下滑,得到一条如图2所示的纸带。O点为打点的第一个点,A、B、C、D、E、F、H是计数点,每相邻两计数点间还有4个点没有标出,OA=17.65cm、AB=11.81cm、BC=14.79cm、CD=17.80cm、DE=20.81cm、EF=23.80cm、FH=26.79cm,根据以上数据进行下列处理。(g=10m/s2)
(1)物块匀加速下滑的加速度是 m/s2,物体所受的合外力是 N。(结果保留三位有效数字)
(2)完成右表:
(3)利用(2)表中的数据,画出下列图象的图线。(按表中的数据小数点后保留两位作图)
(4)根据(2)表中的数据和(3)中的图线,实验结论是
。

从0点到各点的过程 合力所做的功W 单位(J) | 各点的动能EK 单位(J) | ||
OB | 0.8838 | B | 0.8845 |
OC | 1.3275 | C | 1.3276 |
OD | D | 1.8634 | |
OE | 2.4858 | E | |
OF | 3.1998 | F | 3.1992 |

某同学为了探究物体在斜面上运动时摩擦力与斜面倾角的关系,设计实验装置如图。长直平板一端放在水平桌面上,另一端架在一物块上。在平板上标出A、B两点,B点处放置一光电门,用光电计时器记录滑块通过光电门时挡光的时间,
实验步骤如下:
(1)用游标卡尺测测最滑块的挡光长度d,用天平测量滑块的质量m;
(2)用直尺测量A、B之间的距离s,A点到水平桌面的垂直距离h1,B点到水平桌面的垂直距离h2;
(3)将滑块从A点静止释放.由光电计时器读出滑块的挡光时间t;
(4)重复步骤 ③ 数次,井求挡光时间的平均值![]()
(5)利用所测数据求出摩擦力f和斜面倾角的余弦值cosα;
(6)多次改变斜面的倾角,重复实验步骤②③④⑤做出f一cosα关系曲线。
用测量的物理量完成下列各式(重力加速度为g)
(1)斜面倾角的余弦cosα= ;
(2)滑块通过光电门时的速度v = ;
(3)滑块运动时的加速度a= ;
(4)滑块运动时所受到的摩擦阻力f= ;
