0 135639 135647 135653 135657 135663 135665 135669 135675 135677 135683 135689 135693 135695 135699 135705 135707 135713 135717 135719 135723 135725 135729 135731 135733 135734 135735 135737 135738 135739 135741 135743 135747 135749 135753 135755 135759 135765 135767 135773 135777 135779 135783 135789 135795 135797 135803 135807 135809 135815 135819 135825 135833 447348
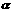 角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直于轨道平面的匀强磁场,磁感应强度为B.一根质量为m的金属杆从轨道上静止自由滑下,经过足够长的时间后,金属杆的速度会趋近于一个最大速度vm,则( )
角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直于轨道平面的匀强磁场,磁感应强度为B.一根质量为m的金属杆从轨道上静止自由滑下,经过足够长的时间后,金属杆的速度会趋近于一个最大速度vm,则( )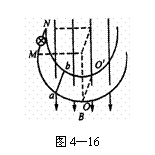

 如图4-15所示,T为理想变压器,A1、A2为交流电流表,R1、R2为定值电阻,R3为滑动变阻器,原线圈两端接恒压交流电源,当滑变阻器的滑动触头向下滑动时( )
如图4-15所示,T为理想变压器,A1、A2为交流电流表,R1、R2为定值电阻,R3为滑动变阻器,原线圈两端接恒压交流电源,当滑变阻器的滑动触头向下滑动时( )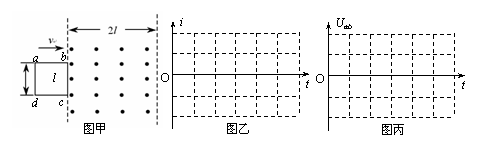

 ︰
︰
 [跟踪练习]
[跟踪练习]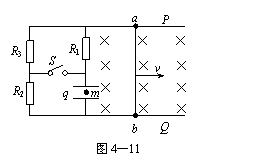
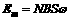 ,最大值
,最大值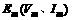 与线圈的形状,以及转轴的位置无关,但转轴应与磁感线垂直.
与线圈的形状,以及转轴的位置无关,但转轴应与磁感线垂直.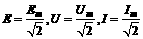 .各种交流电器设备上标准值及交流电表上的测量值都是指有效值.
.各种交流电器设备上标准值及交流电表上的测量值都是指有效值.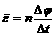
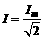 ,其他交流电流的有效值只能根据有效值的定义来计算.
,其他交流电流的有效值只能根据有效值的定义来计算.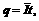 而
而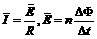 .
.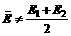 ,平均值不等于有效值.
,平均值不等于有效值. 绕垂直于磁感线的转轴匀速转动,线圈的电阻为R.求:
绕垂直于磁感线的转轴匀速转动,线圈的电阻为R.求: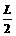 .磁场的磁感强度为B,方向垂直纸面向里.现有一段长度为
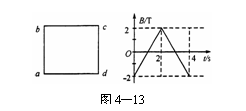
.磁场的磁感强度为B,方向垂直纸面向里.现有一段长度为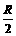 的均匀导体棒MN架在导线框上,开始时紧靠ac,然后沿bc方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触,当MN滑过的距离为
的均匀导体棒MN架在导线框上,开始时紧靠ac,然后沿bc方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触,当MN滑过的距离为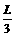 时,导线ac中的电流为多大?方向如何?
时,导线ac中的电流为多大?方向如何?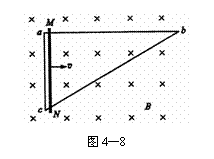
 电能
电能 内能(焦耳热)
内能(焦耳热)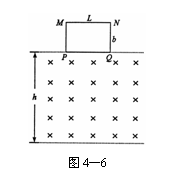
 (2)当ab棒的速度变为初速度的
(2)当ab棒的速度变为初速度的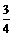 时,cd棒的加速度是多少?
时,cd棒的加速度是多少?