第四章 三角函数
一、角的概念的推广
1.“旋转”形成角,注意:“顶点”“始边”“终边”
2.正角按______方向旋转,负角按______方向旋转,零角。
3.象限角:第一象限角的集合为 ________________________________
第二象限角的集合为 ________________________________
第三象限角的集合为 _________________________________________
第四象限角的集合为 ________________________________
4.终边相同的角:所有与a终边相同的角构成集合 _________
终边在 轴上的角的集合
___________________________________
轴上的角的集合
___________________________________
终边在y轴上的角的集合 ___________________________________
二、弧度制
1.定义:长度等于半径长的圆弧所对的圆心角称为1弧度的角。
2.角a的弧度数的绝对值:
(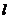 为弧长,
为弧长,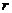 为半径)
为半径)
3.角度制与弧度制的换算:1rad=
4.扇形面积公式:S=
______________(其中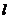 是扇形弧长,
是扇形弧长,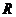 是圆的半径)
是圆的半径)
三、任意角的三角函数
1.定义:设a是一个任意角,在a的终边上任取一点P(x,y),P与原点的距离r=
则sin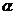 =
cos
=
cos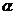 =
tan
=
tan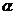 =
cot
=
cot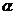 = sec
= sec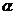 =
csc
=
csc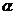 =
=
2.三角函数值在各象限的符号:
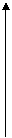 记忆法则:
记忆法则:

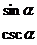 为 全
为 全
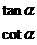 为
为 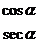 为
为
3.特殊角三角函数值
角α(角度)
0○
30○
45○
60○
90○
180○
270○
360○
角α(弧度)
sin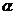
cos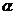
tan
四、同角三角函数的基本关系
1.平方关系: ; ;
2.商数关系: ;
3.倒数关系: ; ;
五、诱导公式
1. sin(k 360°+a) = , cos(k 360°+a) = . tan(k360°+a) = ,
2. sin(180°+a) = , cos(180°+a) = . tan(180°+a) = ,
3. sin(-a) = ___, cos(-a) = __, tan(-a) = ___,
4. sin(180°-a) = , cos(180°-a) = . tan(180°-a) =
5. sin(360°-a) = , cos(360°-a) = . tan(360°-a) = ,
6. sin(90° -a) = , cos(90° -a) = . tan(90° -a) = ,
7. sin(90° +a) = , cos(90° +a) = . tan(90° +a) = ,
8. sin(270° -a) = , cos(270° -a) = . tan(270° -a) = ,
9. sin(270° +a) = , cos(270° +a) = . tan(270° +a) = ,
记忆口诀:
六、两角和与差的三角函数
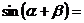 ;
; 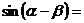 ;
;
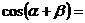 ;
; 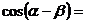 ;
;
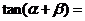 ______ ;
______ ; 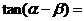 _____
_____
七、二倍角公式
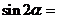 ;
;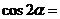 ___= _____=
______;
___= _____=
______;
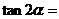
由三角恒等式派生的公式:
1. 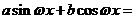
2.(sinα±cosα)2=
3.2cos2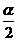 =
=
4.2sin2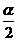 =
=
八、三角函数的图象和性质
函数
y=sinx
y=cosx
y=tanx
图象
定义域
值域
最 值
当x= ymax=1
当x= ymin=-1
当x= ymax =1
当x= ymin=-1
奇偶性
周期
单调性
x∈ 递增
x∈ 递减
x∈ 递增
x∈ 递减
x∈ 递增
九、已知三角函数值求角(用反三角函数表示)
1.已知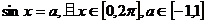 ,
,
①当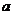 =-1时,x= ____; ②当
=-1时,x= ____; ②当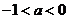 时,x=
;
时,x=
;
③当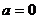 时,x= _____ ; ④当
时,x= _____ ; ④当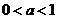 时, x=
;
时, x=
;
⑤当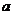 =1时,x= ______;
=1时,x= ______;
2.已知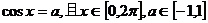 ,
,
①当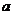 =-1时,x= ____; ②当
=-1时,x= ____; ②当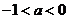 时,x=
;
时,x=
;
③当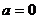 时,x= _____; ④当
时,x= _____; ④当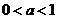 时, x=
;
时, x=
;
⑤当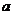 =1时,x= ______;
=1时,x= ______;
3.已知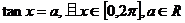 ,
,
①当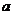 <0时,x=
;②当
<0时,x=
;②当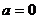 时,x= ______ ;
时,x= ______ ;
③当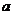 >0时,x=
;
>0时,x=
;
十、函数y=Asin(ωx+φ)的图象
当函数y=Asin(ωx+φ)(A>0,ω>0),x∈[0,+∞]表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做振动的振幅;往往振动一次所需要的时间T=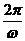 ,它叫做振动的周期;单位时间内往复振动的次数f=
,它叫做振动的周期;单位时间内往复振动的次数f=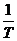 =
=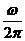 ,它叫做振动的频率;ωx+φ叫做相位,φ叫做初相
,它叫做振动的频率;ωx+φ叫做相位,φ叫做初相
一般地,函数y=Asin(ωx+φ)(A>0,ω>0)(x∈R)的图象可以看作用下面的方法得到:先把y=sinx的图象上的所有的点向 (φ>0)或向 (φ<0)平移 个单位,再把所得各点的横坐标 (ω>1)或 (0<ω<1=到原来的 倍(纵坐标不变),再把所得各点的纵坐标 (A>1)或 (0<A<1=到原来的 倍(横坐标不变).
若是先压缩后平移,此时平移的量为 个单位.