2009年高考数学总复习解题思维专题讲座之二
数学思维的反思性
一、概述
数学思维的反思性表现在思维活动中善于提出独立见解,精细地检查思维过程,不盲从、不轻信。在解决问题时能不断地验证所拟定的假设,获得独特的解决问题的方法,它和创造性思维存在着高度相关。本讲重点加强学生思维的严密性的训练,培养他们的创造性思维。
二、思维训练实例
例1 已知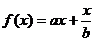 ,若
,若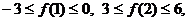 求
求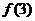 的范围。
的范围。
错误解法 由条件得
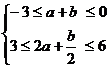

②×2-①得 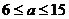
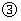
①×2-②得 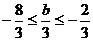
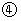
 +
+ 得
得 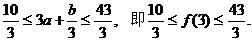
错误分析 采用这种解法,忽视了这样一个事实:作为满足条件的函数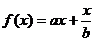 ,其值是同时受
,其值是同时受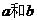 制约的。当
制约的。当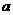 取最大(小)值时,
取最大(小)值时,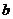 不一定取最大(小)值,因而整个解题思路是错误的。
不一定取最大(小)值,因而整个解题思路是错误的。
正确解法 由题意有
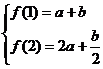
解得: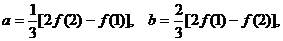
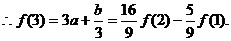
把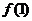 和
和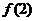 的范围代入得
的范围代入得 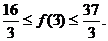
在本题中能够检查出解题思路错误,并给出正确解法,就体现了思维具有反思性。只有牢固地掌握基础知识,才能反思性地看问题。
例2
证明勾股定理:已知在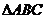 中,
中,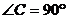 ,求证
,求证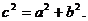
错误证法 在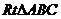 中,
中,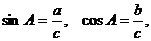 而
而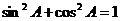 ,
,
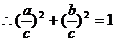 ,即
,即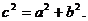
错误分析 在现行的中学体系中,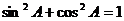 这个公式本身是从勾股定理推出来的。这种利用所要证明的结论,作为推理的前提条件,叫循环论证。循环论证的错误是在不知不觉中产生的,而且不易发觉。因此,在学习中对所学的每个公式、法则、定理,既要熟悉它们的内容,又要熟悉它们的证明方法和所依据的论据。这样才能避免循环论证的错误。发现本题犯了循环论证的错误,正是思维具有反思性的体现。
这个公式本身是从勾股定理推出来的。这种利用所要证明的结论,作为推理的前提条件,叫循环论证。循环论证的错误是在不知不觉中产生的,而且不易发觉。因此,在学习中对所学的每个公式、法则、定理,既要熟悉它们的内容,又要熟悉它们的证明方法和所依据的论据。这样才能避免循环论证的错误。发现本题犯了循环论证的错误,正是思维具有反思性的体现。
(2) 验算的训练
验算是解题后对结果进行检验的过程。通过验算,可以检查解题过程的正确性,增强思维的反思性。
例3
已知数列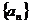 的前
的前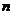 项和
项和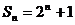 ,求
,求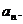
错误解法 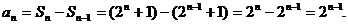
错误分析 显然,当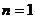 时,
时,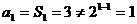 ,错误原因,没有注意公式
,错误原因,没有注意公式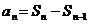 成立的条件是
成立的条件是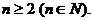 因此在运用
因此在运用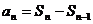 时,必须检验
时,必须检验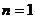 时的情形。即:
时的情形。即: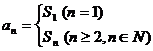
例4
实数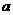 为何值时,圆
为何值时,圆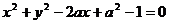 与抛物线
与抛物线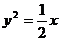 有两个公共点。
有两个公共点。
错误解法 将圆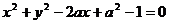 与抛物线
与抛物线 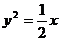 联立,消去
联立,消去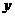 ,
,
得 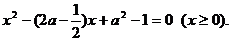 ①
①
因为有两个公共点,所以方程①有两个相等正根,得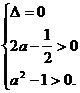
解之,得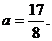
错误分析 (如图2-2-1;2-2-2)显然,当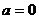 时,圆与抛物线有两个公共点。
时,圆与抛物线有两个公共点。
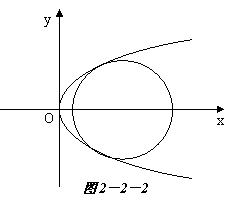
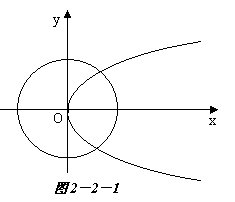
要使圆与抛物线有两个交点的充要条件是方程①有一正根、一负根;或有两个相等正根。
当方程①有一正根、一负根时,得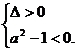 解之,得
解之,得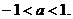
因此,当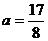 或
或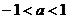 时,圆
时,圆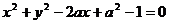 与抛物线
与抛物线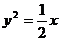 有两个公共点。
有两个公共点。
思考题:实数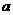 为何值时,圆
为何值时,圆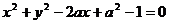 与抛物线
与抛物线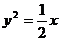 ,
,
(1) 有一个公共点;
(2) 有三个公共点;
(3) 有四个公共点;
(4) 没有公共点。
养成验算的习惯,可以有效地增强思维反思性。如:在解无理方程、无理不等式;对数方程、对数不等式时,由于变形后方程或不等式两端代数式的定义域可能会发生变化,这样就有可能产生增根或失根,因此必须进行检验,舍弃增根,找回失根。
(3) 独立思考,敢于发表不同见解
受思维定势或别人提示的影响,解题时盲目附和,不能提出自己的看法,这不利于增强思维的反思性。因此,在解决问题时,应积极地独立思考,敢于对题目解法发表自己的见解,这样才能增强思维的反思性,从而培养创造性思维。
例5 30支足球队进行淘汰赛,决出一个冠军,问需要安排多少场比赛?
解 因为每场要淘汰1个队,30个队要淘汰29个队才能决出一个冠军。因此应安排29场比赛。
思 路 分 析 传统的思维方法是:30支队比赛,每次出两支队,应有15+7+4+2+1=29场比赛。而上面这个解法没有盲目附和,考虑到每场比赛淘汰1个队,要淘汰29支队,那么必有29场比赛。
例6
解方程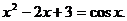
考察方程两端相应的函数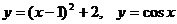 ,它们的图象无交点。
,它们的图象无交点。
所以此方程无解。
例7 设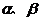 是方程
是方程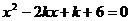 的两个实根,则
的两个实根,则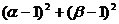 的最小值是( )
的最小值是( )

思路分析 本例只有一个答案正确,设了3个陷阱,很容易上当。
利用一元二次方程根与系数的关系易得: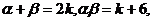
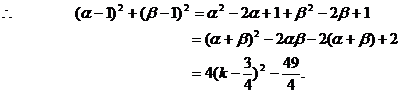
有的学生一看到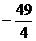 ,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
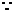 原方程有两个实根
原方程有两个实根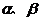 ,
,
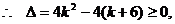
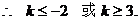
当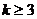 时,
时,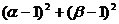 的最小值是8;当
的最小值是8;当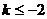 时,
时,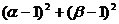 的最小值是18;
的最小值是18;
这时就可以作出正确选择,只有(B)正确。