2006-2007学年度烟台市招远第二学期第一学段考试
初三数学试题
说明:
1.本试卷试题共115分;
2.书写质量3分;
3.卷面安排2分.
整个试卷满分为120分.
一、选择题:(将唯一正确答案代号填在括号内.每小题2分.满分30分)
1.下列方程属于一元二次方程的是 ( )
A. B.
B.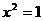
C.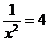 D.
D.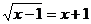
2.下列命题中,不正确的是 ( )
A.全等三角形的面积相等
B.全等三角形的对应边相等
C.全等三角形的对应角相等
D.由两边和其中一个角对应相等的两个三角形全等
3.方程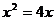 的解是
( )
的解是
( )
A.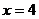 B.
B.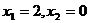
C.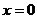 D.
D.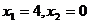
4.已知△ABC的三边分别为a.b、c,则下列条件中不能判定△ABC是直角三角形的是 ( )
A.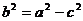 B.
B.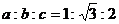
C.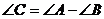 D.
D.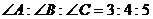
5.若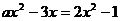 是关于
是关于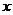 的一元二次方程,则
( )
的一元二次方程,则
( )
A.a≠0 B.a=2 C.a≠2 D.a为任意实数
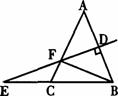
6.如图,在△ABD和△BAC中,∠l=∠2,∠C=∠D,AC、BD相交于点E,则下烈结论中正确的个数有 ( )

①∠DAE=∠CBE; ②△ADE≌△BCE;
③CE=DE; ④△EAB为等腰三角形
A.1个 B.2个 C.3个 D.4个
7.已知关于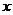 的一元二次方程
的一元二次方程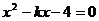 的一个根为2,则另一根是
( )
的一个根为2,则另一根是
( )
A.-2 B.1 C.2 D.4
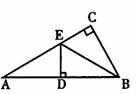
8.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是 ( )
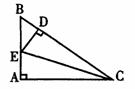
A.AE=BE B.DB=DE
C.AE=BD D.∠BCE=∠ACE
9.方程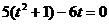 根的情况是
( )
根的情况是
( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.以上说法都不正确
10.小颖在做数学作业时,因钢笔漏水,不小心将部分字迹污损了,作业过程如下(涂黑部分即污损部分).
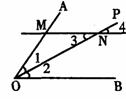
已知:如图,OP平分∠AOB,MN∥OB,交OA于M、交OP于N.
求证:OM=NM.
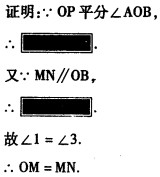
小颖知道:污损部分的内容分别为以下四项中的两项,①∠1=∠2,②∠2=∠3,③∠3=∠4,④∠4=∠1,那么污损部分内容应是 ( )
A.①② B.②③ C.①④ D.③④
11.如果分式 的值是零,则
的值是零,则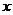 的值一定是
( )
的值一定是
( )
A.-2 B.2 C.±2 D.不等于2
12.等腰三角形顶角为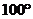 ,两腰的垂直平分线交于点P,则
( )
,两腰的垂直平分线交于点P,则
( )
A.点P在三角形内 B.点P在三角形底边上
C.点P在三角形外 D.点P的位置与三角形的形状无关
13.某种型号电视机经过连续两次降价,每台售价由原来的1500元降到了980元.设平均每次降价的百分率为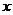 ,则以下所列方程正确的是 ( )
,则以下所列方程正确的是 ( )
A.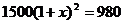 B.
B.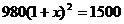
C.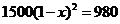 D.
D.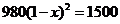
14.如图,在△ABC中,∠C=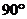 ,BE平分∠B交AC于点E,DE是斜边AB的垂直平分线,D为垂足.若DE=1cm,则AC的长为
( )
,BE平分∠B交AC于点E,DE是斜边AB的垂直平分线,D为垂足.若DE=1cm,则AC的长为
( )
A.2cm B.3cm C.3.5cm D.4cm
15.在一次小型会议上,参加会议的代表每人都和其他代表握手一次,共握手36次,则参加这次会议的人数是 ( )
A.9人 B.10人 C.12人 D.18人
二、填空题:(将正确答案填在横线上.每小题3分.满分30分)
16.把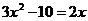 表示成一元二次方程的一般形式后,它的一次项系数是______;常数项是__________.
表示成一元二次方程的一般形式后,它的一次项系数是______;常数项是__________.
17.命题“全等三角形的对应角相等”的逆命题是:_________________,它是___________命题(填“真”或“假”).
18.一元二次方程有一个根是-3,请写出这样的一个方程_____________________.
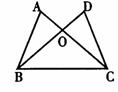
19.如图,在△ABC和△DCB中,AB=DC,AC与BD相交于O,要使△ABO≌△DCO,需补充的一个条件是_________________(只填写一个你认为合适的条件)
20.写出一个两根分别为2和-3的一元二次方程是____________________.
21.如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D、交BC的延长线于点E、交AC于点F.若AB+BC=10cm,则△BCF的周长是_________cm.
22.若关于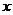 的一元二次方程
的一元二次方程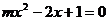 有实数根,则m的取值范围是________.
有实数根,则m的取值范围是________.
23.如图,在△ABC中,∠C=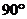 ,∠A的平分线交BC于D点,BC=21cm,BD:DC=4:3,则点D到AB的距离为___________.
,∠A的平分线交BC于D点,BC=21cm,BD:DC=4:3,则点D到AB的距离为___________.
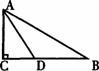
24.用一块长80cm,宽60cm的薄钢片,在四个角上各截去一个边长为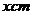 的小正方形,然后做成底面积为l500
的小正方形,然后做成底面积为l500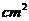 的没有盖的长方体盒子,为了求出
的没有盖的长方体盒子,为了求出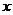 ,根据题意列方程并整理后得___________________.
,根据题意列方程并整理后得___________________.
25.如图,在△ABC中,AB=AC,∠B=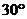 ,点D在BC上,且AD⊥AC.若AD=1,则BC的长为____________.
,点D在BC上,且AD⊥AC.若AD=1,则BC的长为____________.
三、解方程:(每小题5分。满分l0分)
26.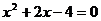 (用配方法解);
(用配方法解);
27.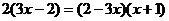 .
.
四、解答题:(每小题6分,满分l8分)
28.已知关于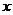 的方程
的方程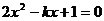 的一个根与方程
的一个根与方程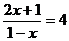 的解相同.
的解相同.
(1)求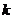 的值
的值
(2)求方程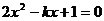 的另一个根.
的另一个根.
29.某水果批发商场经销一种高档水果,如果每千克盈利l0元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克每涨价l元,日销售量将减少20 千克.现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
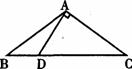
30.如图,在梯形ABCD中,AD∥BC,AB=DC=4,AD=3,BC=7.求∠B的度数.
31.为解方程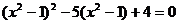 ,我们可将
,我们可将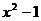 看作一个整体,然后设
看作一个整体,然后设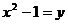 ;那么原方程可化为
;那么原方程可化为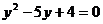 ①,解这个方程,得
①,解这个方程,得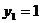 ,
,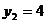 .当
.当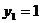 时,
时,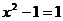 ,所以
,所以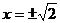 ;当
;当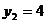 时,
时,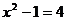 ,所以
,所以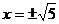 则原方程的解为
则原方程的解为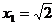 ,
,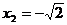 ,
,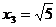 ,
,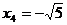
解答下列问题:
(1)填空:在由原方程得到方程①的过程中,利用_________法达到降次的目的,体现了__________的数学思想;
(2)请利用上述方法解方程: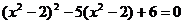 .
.
六、探索题:(第32题6分。第33题l2分.满分l8分)
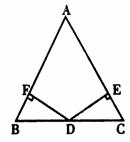
32.如图,D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E、F,且DE=DF.试判断△ABC的形状,并给出证明.
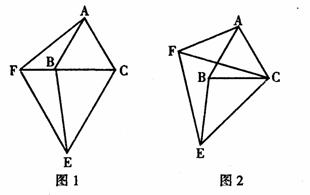
33.如图l,△ABC和△CEF是两个边长不等的等边三角形,且有一个公共顶点C,连结AF和BE.
(1)线段AF和BE有怎样的大小关系?请证明你的结论;
(2)将图l中的△CEF绕点C旋转一定的角度,得到图2,(1)中的结论还成立吗? 作出判断并说明理由;
(3)若将图1中的△ABC绕点C旋转一定的角度,请你画出一个变换后的图形(草图即可),(1)中的结论还成立吗?作出判断不必说明理由;
(4)根据以上证明、说理、画图,归纳你的发现.