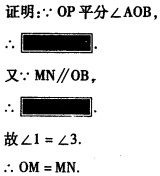
摘要:已知:如图.OP平分∠AOB.MN∥OB.交OA于M.交OP于N.求证:OM=NM.
网址:http://m.1010jiajiao.com/timu_id_671636[举报]
如图,已知∠AOB和一条定长线段a,在∠AOB内找一点P,使P到角的两边OA、OB的距离都等于a.
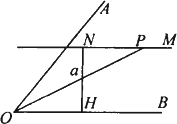
作法:①在∠AOB内作OB的垂线段NH,使NH=a,H为垂足;②过N作NM∥OB;③作∠AOB的平分线OP,与MN交于点P;④点P即为所求,其中③的依据是
[ ]
A.平行线间的距离处处相等
B.到角的两边等距离的点在角的平分线上
C.角的平分线上的点到角的两边等距离
D.到线段两端等距离的点在这条线段的垂直平分线上
小颖在做数学作业时,因钢笔漏水,不小心将部分字迹污损了,作业过程如下(涂黑部分即污损部分).
已知:如图,OP平分∠AOB,MN∥OB,交OA于M、交OP于N.求证:OM=NM.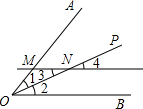
小颖知道:污损部分的内容分别为以下四项中的两项,①∠1=∠2,②∠2=∠3,③∠3=∠4,④∠4=∠1,那么污损部分内容应是( )
已知:如图,OP平分∠AOB,MN∥OB,交OA于M、交OP于N.求证:OM=NM.


小颖知道:污损部分的内容分别为以下四项中的两项,①∠1=∠2,②∠2=∠3,③∠3=∠4,④∠4=∠1,那么污损部分内容应是( )
查看习题详情和答案>>
小颖在做数学作业时,因钢笔漏水,不小心将部分字迹污损了,作业过程如下(涂黑部分即污损部分).
已知:如图,OP平分∠AOB,MN∥OB,交OA于M、交OP于N.求证:OM=NM.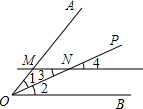

小颖知道:污损部分的内容分别为以下四项中的两项,①∠1=∠2,②∠2=∠3,③∠3=∠4,④∠4=∠1,那么污损部分内容应是
- A.①②
- B.②③
- C.①④
- D.③④
小颖在做数学作业时,因钢笔漏水,不小心将部分字迹污损了,作业过程如下(涂黑部分即污损部分).已知:如图,OP平分∠AOB,MN∥OB,交OA于M、交OP于N.求证:OM=NM。

小颖知道:污损部分的内容分别为以下四项中的两项,①∠1=∠2,②∠2=∠3,③∠3=∠4,④∠4=∠1,那么污损部分内容应是

小颖知道:污损部分的内容分别为以下四项中的两项,①∠1=∠2,②∠2=∠3,③∠3=∠4,④∠4=∠1,那么污损部分内容应是
[ ]
A.①②
B.②③
C.①④
D.③④
查看习题详情和答案>>
B.②③
C.①④
D.③④
(2013•连云港)小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连接AE并延长交BC的延长线于点F,求证:S四边形ABCD=S△ABF(S表示面积)
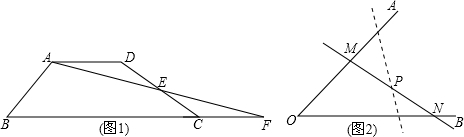
问题迁移:如图2:在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
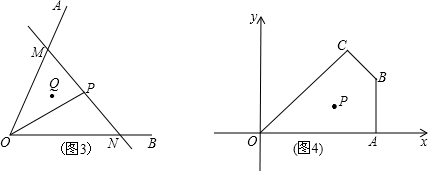
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66°,∠POB=30°,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66°≈0.91,tan66°≈2.25,
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)(6,3)(
,
)、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
查看习题详情和答案>>
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连接AE并延长交BC的延长线于点F,求证:S四边形ABCD=S△ABF(S表示面积)

问题迁移:如图2:在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,请问当直线MN在什么位置时,△MON的面积最小,并说明理由.

实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66°,∠POB=30°,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66°≈0.91,tan66°≈2.25,
| 3 |
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)(6,3)(
| 9 |
| 2 |
| 9 |
| 2 |