摘要：(2)请利用上述方法解方程:．六.探索题:(第32题6分.第33题l2分．满分l8分)
网址：http://m.1010jiajiao.com/timu_id_671670[举报]
为解方程（x2-1）2-5（x2-1）+4=0，我们可将x2-1看作一个整体，然后设x2-1=y；那么原方程可化为y2-5y+4=0①，解这个方程，得y1=1，y2=4．当y1=1时，x2-1=1，所以x=±
；当y2=4时，x2-1=4，所以x=±
则原方程的解为x1=
，x2=-
，x3=
，x4=-
解答下列问题：
（1）填空：在由原方程得到方程①的过程中，利用
（2）请利用上述方法解方程：（x2-2）2-5（x2-2）+6=0．
查看习题详情和答案>>
| 2 |
| 5 |
| 2 |
| 2 |
| 5 |
| 5 |
解答下列问题：
（1）填空：在由原方程得到方程①的过程中，利用
换元
换元
法达到降次的目的，体现了转化
转化
的数学思想；（2）请利用上述方法解方程：（x2-2）2-5（x2-2）+6=0．
为解方程（x2-1）2-5（x2-1）+4=0，我们可将x2-1看作一个整体，然后设x2-1=y；那么原方程可化为y2-5y+4=0①，解这个方程，得y1=1，y2=4．当y1=1时，x2-1=1，所以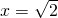
；当y2=4时，x2-1=4，所以
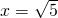则原方程的解为
，
，
，
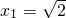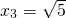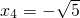
解答下列问题：
（1）填空：在由原方程得到方程①的过程中，利用______法达到降次的目的，体现了______的数学思想；
（2）请利用上述方法解方程：（x2-2）2-5（x2-2）+6=0．
查看习题详情和答案>>
阅读材料：为解方程（x2-1）2-5（x2-1）+4=0，我们可以将x2-1看作一个整体，然后设x2-1=y，那么原方程可化为y2-5y+4=0.……①
解得y1=1，y2=4，
当y=1时，x2-1=1，
∴x2=2，
∴
，
当y=4时，x2-1=4，
∴x2=5，
∴
，
故原方程的解为x1=
。
解答问题：
（1）上述解题过程，在由原方程得到方程①的过程中，利用____法达到了降次的目的，体现了转化的数学思想；
（2）请利用上述方法解方程：（x2﹣2）2﹣5（x2﹣2）+6=0。
查看习题详情和答案>>
解得y1=1，y2=4，
当y=1时，x2-1=1，
∴x2=2，
∴
，当y=4时，x2-1=4，
∴x2=5，
∴
，故原方程的解为x1=
。解答问题：
（1）上述解题过程，在由原方程得到方程①的过程中，利用____法达到了降次的目的，体现了转化的数学思想；
（2）请利用上述方法解方程：（x2﹣2）2﹣5（x2﹣2）+6=0。