天津市河北区2007届高三第一次模拟考试数学理科试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题列出的四个选项中,只有一项是符合题目要求的.
1. 集合A={x|-3<x<5},B={x|x<1或x>4},则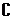 RA∩
RA∩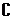 R B是( )
R B是( )
A.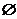 B.{x|-3≤x≤5}
B.{x|-3≤x≤5}
C.{x|-3≤x≤1或4≤x≤5} D.{x|x≤-3或1≤x≤4或x≥5}
2. 函数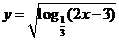 的定义域为( )
的定义域为( )
A.(-∞,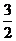 ) B.(
) B.(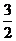 ,+∞) C.(
,+∞) C.(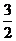 ,2] D.(
,2] D.(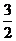 ,2)
,2)
3. 设数列{an}是等差数列,且a2=-9,a7=11,Sn是数列{an}是的前n项和,则( )
A.S7=S8
B.S8>
4. 把函数y=cos(x+ )的图象向右平移φ个单位,所得的图象正好关于y轴对称,
)的图象向右平移φ个单位,所得的图象正好关于y轴对称,
则φ的最小正值为( )
A.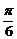 B.
B. C.
C. D.
D.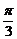
5. 已知a、b为向量,下列命题中正确的是( )
A. B.若
B.若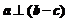 ,则
,则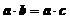
C.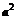 ≥
≥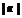 D.
D.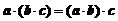
6.
点P(x,y)在以A(-3,1),B(-1,0),C(-2,-2)为顶点的△ABC的内部运动(不包含边界),则 的取值范围是(
)
的取值范围是(
)
A.[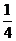 ,
,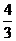 ] B.(1,
] B.(1,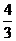 ) C.(
) C.(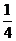 ,
,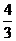 ) D.(
) D.(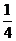 ,1)
,1)
7. 三棱锥P―ABC中,PA、PB、PC两两垂直且PA=2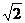 ,PB=4,PC=2
,PB=4,PC=2 ,如果三棱锥的四个顶点都在同一球面上,那么这个球的球心到直线PB的距离为( )
,如果三棱锥的四个顶点都在同一球面上,那么这个球的球心到直线PB的距离为( )
A.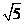 B.5 C.
B.5 C.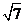 D.
D. 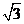
8. 曲线y2=4x上的点P到点A(-2,4)与到y轴的距离之和为d,则d的最小值是 ( )
A.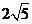 B.3 C.4
D.5
B.3 C.4
D.5
9. 某运输公司有7个车队,每个车队的车都多于4辆且这7个车队的车型号都相同,要从这7个车队中抽出10辆车组成一运输车队,每个队至少抽1辆车,则不同抽法的种数为( )
A.7 B.28 C.35 D.84
10.若f(x)是R上的减函数,且f(x)的图象经过点A(0,4)和点B(3,-2),则当不等式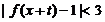 的解集为(-1,2)时,t的值为(
)
的解集为(-1,2)时,t的值为(
)
A.-1 B.0 C.1 D.2
二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.
11.复数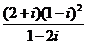 的值是__________ .
的值是__________ .
12.以原点为圆心,且截直线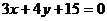 所得弦长为8的圆的方程是___________ .
所得弦长为8的圆的方程是___________ .
13.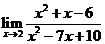 的值等于_________________ .
的值等于_________________ .
14.使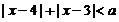 有实数解的a的取值范围是_________________.
有实数解的a的取值范围是_________________.
15.已知-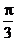 ≤x≤
≤x≤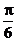 ,要使
,要使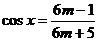 成立,则实数m的取值范围是__________.
成立,则实数m的取值范围是__________.
16.如果方程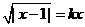 恰有唯一解,则实数k的取值范围是___________________.
恰有唯一解,则实数k的取值范围是___________________.
三、解答题:本大题共6小题,共76分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)已知函数f(x)=cos4x-2sinxcosx-sin4x.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)的对称轴方程;
(Ⅲ)求f(x)的单调递减区间.
18.(本小题满分12分)从一批含有13只正品,2只次品的产品中不放回地抽取3次,每次抽取一只,设抽得次品数为 . (Ⅰ)求
. (Ⅰ)求 的分布列;(Ⅱ)求E
的分布列;(Ⅱ)求E .
.
19.(本小题满分12分)
已知函数f(x)=ax4+bx2+c的图象经过点(0,2),且在x=1处的切线方程
是y=-4x+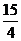 .
.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调递减区间;
(Ⅲ)求函数y=f(x)在区间[-4,1]上的最值.
20.(本小题满分12分)
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.
 E是PD的中点.
E是PD的中点.
(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)求二面角E-AC-D所成平面角的余弦值;
(Ⅲ)求B点到平面EAC的距离.
21.(本小题满分14分)已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、第十四项分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=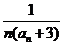 (n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有Sn>
(n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有Sn>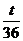 总成立?若存在,求出t;若不存在,请说明理由.
总成立?若存在,求出t;若不存在,请说明理由.
22.(本小题满分14分)已知椭圆C的方程为 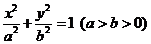 ,过其左焦点F1(-1,0)斜率为1的直线交椭圆于P、Q两点.
,过其左焦点F1(-1,0)斜率为1的直线交椭圆于P、Q两点.
(Ⅰ)若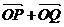 与
与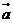 =(-3,1)共线,求椭圆C的方程;
=(-3,1)共线,求椭圆C的方程;
(Ⅱ)已知直线l: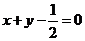 ,在l上求一点M,使以椭圆的焦点为焦点且过M点的双曲线E的实轴最长,求点M的坐标和此双曲线E的方程.
,在l上求一点M,使以椭圆的焦点为焦点且过M点的双曲线E的实轴最长,求点M的坐标和此双曲线E的方程.
天津市河北区2007届高三第一次模拟考试数学理科解答
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
B
D
B
C
A
C
D
C
二、填空题:本大题共6小题,每小题4分,共24分.
11.2
12.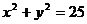 13.
13.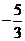
14.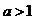 15.m≥
15.m≥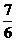 16.k∈(-∞,0]∪(
16.k∈(-∞,0]∪(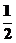 ,+∞)
,+∞)
三、解答题:本大题共6小题,共76分.
17.(本小题满分12分)
解:(Ⅰ) f(x)=(cos4x-sin4x)-2sinx?cosx=(cos2x-sin2x)-sin2x
=cos2x-sin2x=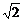 cos(2x+
cos(2x+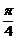 ). …………………………
4分
). …………………………
4分
∴f(x)的最小正周期T=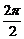 =π. …………………………………… 6分
=π. …………………………………… 6分
(Ⅱ)2x+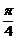 =kπ,则x=
=kπ,则x=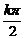 -
-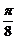 ,k∈Z.
,k∈Z.
∴函数f(x)的对称轴方程是x=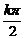 -
-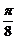 ,k∈Z.
…………………… 8分
,k∈Z.
…………………… 8分
(Ⅲ)令2kπ≤2x+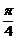 ≤2kπ+π, ………………………………………… 10分
≤2kπ+π, ………………………………………… 10分
则kπ-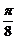 ≤x≤kπ+
≤x≤kπ+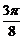 ,k∈Z.
,k∈Z.
故f(x)的单调递减区间为[kπ-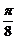 ,kπ+
,kπ+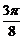 ],k∈Z. …………
12分
],k∈Z. …………
12分
18.(本小题满分12分)
解:(Ⅰ) 的分布如下:
的分布如下:

0
1
2
P
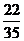
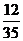
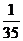
…………………………………………………………6分
(Ⅱ)由(Ⅰ)知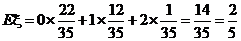 .……………………12分
.……………………12分
19.(本小题满分12分)
解:(Ⅰ)由题意知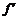 (x)=4ax3+2bx, …………………………………… 2分
(x)=4ax3+2bx, …………………………………… 2分
f(0)=2,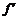 (1)=-4,f(1)=-
(1)=-4,f(1)=-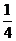 ,
,
∴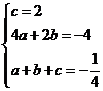 . ………………………………………………………… 4分
. ………………………………………………………… 4分
∴a=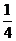 ,b=-
,b=-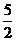 ,c=2.
,c=2.
∴f(x)=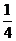 x4-
x4-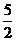 x2+2. ………………………………………………… 6分
x2+2. ………………………………………………… 6分
(Ⅱ)∵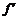 (x)=x3-5x, ……………………………………………………… 7分
(x)=x3-5x, ……………………………………………………… 7分
由x3-5x<0,得x∈(-∞,-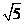 )∪(0,
)∪(0,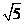 ),
),
∴f(x)的单调递减区间为(-∞,-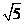 )和(0,
)和(0,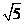 ). ……………… 9分
). ……………… 9分
(Ⅲ)∵在区间[-4,1]上有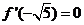 ,
,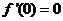 ,…………………… 10分
,…………………… 10分
∴解得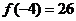 ,
,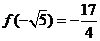 ,
,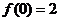 ,f(1)=-
,f(1)=-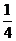 .
.
∴在区间[-4,1]上函数y=f(x)的最大值为26,最小值为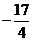 . … 12分
. … 12分
20.(本小题满分12分)
解:(Ⅰ)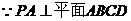 ,
,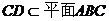 ,
,
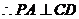 . ……………………………………………………………… 2分
. ……………………………………………………………… 2分

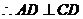
而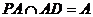
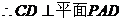 .
.
∵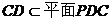 ,
,
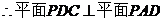 .
………………………………………………… 4分
.
………………………………………………… 4分
(Ⅱ)取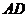 中点
中点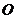 , 连结
, 连结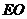 , 则
, 则 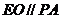 ,
,
∵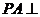 平面
平面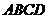 ,
,
∴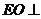 平面
平面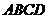 ,
,
过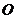 作
作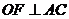 交
交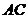 于
于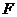 ,连结
,连结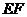 ,
,
则 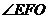 就是二面角
就是二面角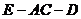 所成平面角.
………………………… 6分
所成平面角.
………………………… 6分
由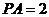 ,则
,则 .
.
在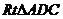 中,
中,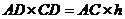 解得
解得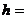
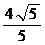
因为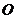 是
是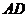 的中点,所以
的中点,所以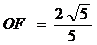 . ……………………………… 7分
. ……………………………… 7分
而 ,由勾股定理可得
,由勾股定理可得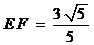 . ……………………………… 8分
. ……………………………… 8分
∴ . ……………………………… 9分
. ……………………………… 9分
(Ⅲ)连结BE,在三棱锥B-EAC中,
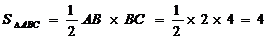 , …………………………… 10分
, …………………………… 10分
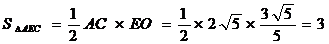 . ………………… 11分
. ………………… 11分
点E到底面BAC的距离EO=1,
则由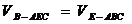 ,即
,即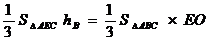 ,
,
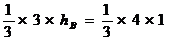 求得
求得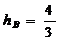 .
.
所以B点到平面EAC的距离是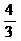 . ……………………………………… 12分
. ……………………………………… 12分
21.(本小题满分14分)
解:(Ⅰ)由题意得(a1+d)(a1+13d)=(a1+4d)2, ……………………… 2 分
整理得2a1d=d2.
∵a1=1,解得(d=0舍),d=2. ………………………………………… 4 分
∴an=2n-1(n∈N*). …………………………………………………… 6 分
(Ⅱ)bn=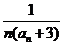 =
= =
= (
(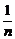 -
-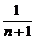 ),
),
∴Sn=b1+b2+…+bn= [(1-
[(1- )+(
)+( -
-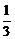 )+…+(
)+…+(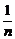 -
-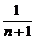 )]
)]
= (1-
(1-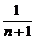 )=
)=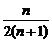 . …………………………………… 10 分
. …………………………………… 10 分
假设存在整数t满足Sn>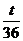 总成立.
总成立.
又Sn+1-Sn=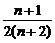 -
-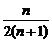 =
=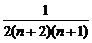 >0,
>0,
∴数列{Sn}是单调递增的. ……………………………………………… 12 分
∴S1=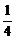 为Sn的最小值,故
为Sn的最小值,故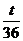 <
<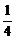 ,即t<9.
,即t<9.
又∵t∈N*,
∴适合条件的t的最大值为8. ………………………………………… 14 分
22.(本小题满分14分)
解:(Ⅰ)将直线PQ的方程为 ,
,
化简得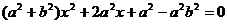 .
.
令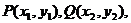 则
则 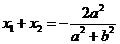 . ……………………… 2分
. ……………………… 2分
由 ,
, 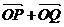 与
与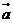 =(-3,1)共线,得
=(-3,1)共线,得
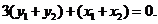 ∴
∴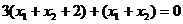 .
.
∴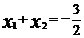 ,即
,即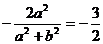 ,∴
,∴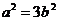 . ………………… 4分
. ………………… 4分
又∵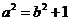 , ∴
, ∴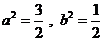 .
.
所以椭圆C的方程为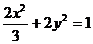 . ……………………………………
6分
. ……………………………………
6分
(Ⅱ)设椭圆C的右焦点为F2,则易知F1(-1,0)F2(1,0),
直线l的方程为: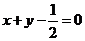 ,因为M在双曲线E上,要双曲线E的实轴最大,只须||MF1|-|MF2||最大, …………………………………………………… 8分
,因为M在双曲线E上,要双曲线E的实轴最大,只须||MF1|-|MF2||最大, …………………………………………………… 8分
设F2(1,0)关于直线l的对称点为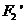 ,
,
则可求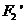 (
(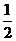 ,-
,-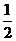 ),则直线
),则直线 与直线l的交点为所求M,
与直线l的交点为所求M,
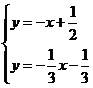 得M(
得M(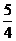 ,-
,- ). ……………………………………… 10分
). ……………………………………… 10分
又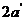 =||MF1|-|MF2||=||MF1|-|M
=||MF1|-|MF2||=||MF1|-|M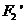 ||≤
||≤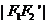 =
=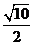 , ……… 12分
, ……… 12分
∴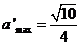 ,
,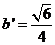 .
.
故所求双曲线E方程为: 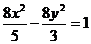 . ……………………………… 14分
. ……………………………… 14分