2006―2007学年度四川省成都市高中毕业班第一次诊断性检测
数学试题(理科)
注意事项:全卷满分为150分,完成时间为120分钟.
参考公式:如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)

如果事件A、B相互独立,那么 其中R表示球的半径
P(A?B)=P(A)?P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P,

那么n次独立重复试验中恰好发生k次的概率
 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共计60分。在每小题列出的4个选项中,只有一项是符合题目要求的,把正确选项代号涂在机读卡的相应位置上.
1.某校现有高一学生210人,高二学生270人,高三学生300人,学校学生会用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那从高三学生中抽取的人数应为 ( )
A.10 B.
|
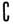 U
U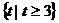 B.
B.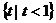 C.
C.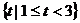 D.
D.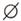
 则不等式
则不等式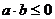 的解集为 ( )
的解集为 ( )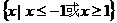 B.
B.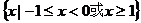
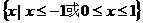 D.
D.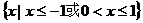
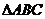 中,“
中,“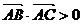 ”是“
”是“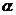 、
、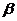 、
、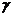 是两两不重合的平面,给出下列命题:①若
是两两不重合的平面,给出下列命题:①若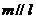 ,
,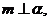 则
则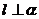 ;②若
;②若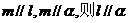 ;③若
;③若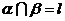 ,
,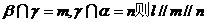 ;④若
;④若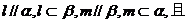 直线l、m为异面直线,则
直线l、m为异面直线,则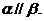 ( )
( )

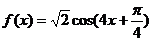
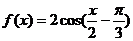

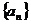 的公比为
的公比为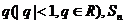 为其前n项和
为其前n项和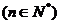 ,又
,又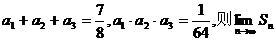 的值为 ( )
的值为 ( )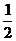 B.
B.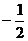 C.
C.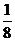 D.1
D.1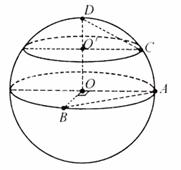
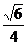 B.
B.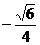
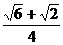 D.
D.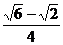
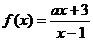 的反函数为
的反函数为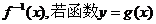 的图象与函数
的图象与函数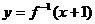 的图象关于直线
的图象关于直线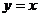 对称,且
对称,且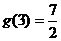 ,则实数a的值为( )
,则实数a的值为( )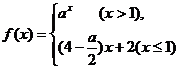 是R上的单调函数,则实数
是R上的单调函数,则实数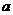 取值范围为( )
取值范围为( )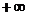 ) B.(1,8) C.(4,8) D.
) B.(1,8) C.(4,8) D.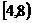
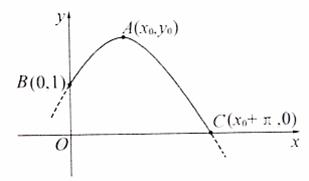
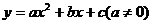 的对称轴在y轴的左侧,其中
的对称轴在y轴的左侧,其中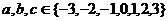 ,在这些抛物线中,记随机变量
,在这些抛物线中,记随机变量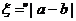 的取值
的取值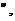 则
则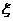 的数学期望值
的数学期望值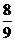 B.
B.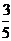 C.
C.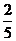 D.
D. 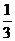
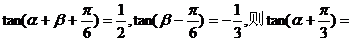 .
.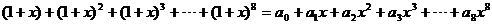 ,则
,则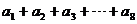 =
.
=
.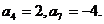 现从
现从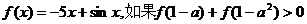 ,
,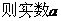 的取值范围为
.
的取值范围为
.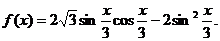
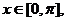 求函数
求函数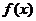 的值域;
的值域;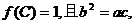
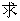
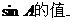
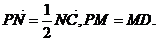 .
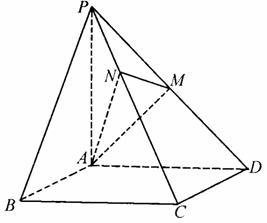
.
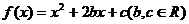 满足
满足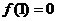 ,且关于x的方程
,且关于x的方程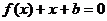 的两个实数根分别在区间(-3,-2),(0,1)内.
的两个实数根分别在区间(-3,-2),(0,1)内.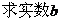 的取值范围;
的取值范围;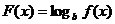 在区间(-1-c,1-c)上具有单调性,求实数c的取值范围.
在区间(-1-c,1-c)上具有单调性,求实数c的取值范围.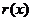 (件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系:
(件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系: ;在销售淡季近似地符合函数关系:
;在销售淡季近似地符合函数关系: 、
、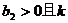 、
、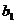 、
、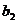 为常数;
为常数;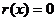 时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
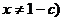 ,
,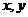 所满足的关系式记为
所满足的关系式记为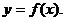 若函数
若函数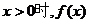 有最小值
有最小值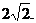
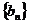 满足如下关系:
满足如下关系:
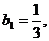 求数列
求数列
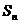 .
.
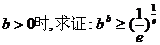 (其中e=2.718
28…是自然对数的底数);
(其中e=2.718
28…是自然对数的底数);
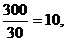 选A.
选A.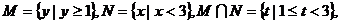 选C.
选C.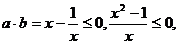 选D.
选D.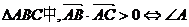 为锐角,不一定为锐角三角形;若
为锐角,不一定为锐角三角形;若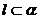 ,错误;③l还需与
,错误;③l还需与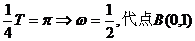 验证可知,选C.
验证可知,选C.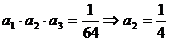 ,
,
 选B.
选B. 种,选B.
种,选B.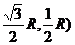 ,D(0,0,R),
,D(0,0,R), 选A.
选A. 中的
中的 选A.
选A. 上是单调弟增函数知
上是单调弟增函数知 同时成立,解不等式组得
同时成立,解不等式组得 ,选D.
,选D.


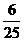 .由
.由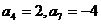 可得等差数列
可得等差数列 2,…,10);由题意,三次取数相当于三次独立重复试验,在每次试验中取得正数的概率为
2,…,10);由题意,三次取数相当于三次独立重复试验,在每次试验中取得正数的概率为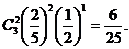
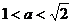 .
.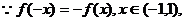
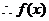 为奇函数;又
为奇函数;又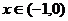 时
时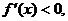
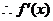 在(-1,0)上是单调递减函数.由奇数的性质可知
在(-1,0)上是单调递减函数.由奇数的性质可知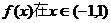 上为单调递减函数;
上为单调递减函数;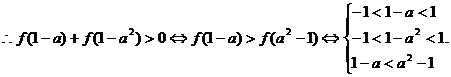

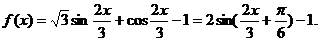 ………………3分
………………3分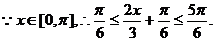
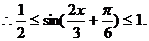

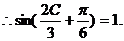
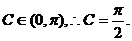 ……………………2分
……………………2分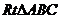 中,
中,
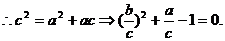

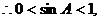
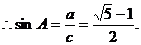 …………………………3分
…………………………3分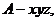 又PA=AD=2,
又PA=AD=2,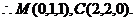
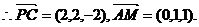
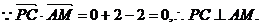 ………………4分
………………4分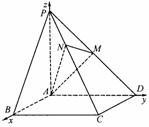

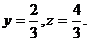
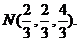 …………………………3分
…………………………3分


 ………………………………1分
………………………………1分
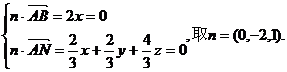


 …………4分
…………4分 …………………………2分
…………………………2分
 …………4分
…………4分
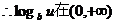 是减函数.
是减函数.
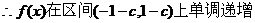
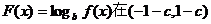 上为减函数.………………2分
上为减函数.………………2分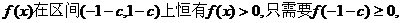
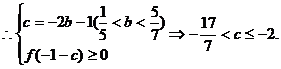 ………………4分
………………4分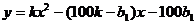
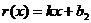
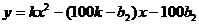
 可知,
可知,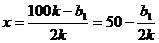 时,利润y取最大值;
时,利润y取最大值; 时,利润y取最大值.
时,利润y取最大值. 时,利润y取最大值.
时,利润y取最大值.
 知,在销售旺季,衬衣的“临界价格”为180元/件.……4分
知,在销售旺季,衬衣的“临界价格”为180元/件.……4分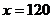 元/件时,销售量为
元/件时,销售量为

 元/件时,利润y取最大值.
元/件时,利润y取最大值.
 …………2分
…………2分

 …………3分
…………3分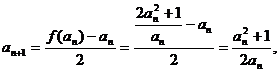

 …………3分
…………3分 (n∈N*). …………1分
(n∈N*). …………1分
 ①
① ②
②

 …………1分
…………1分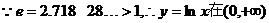 上是单调递增函数.
上是单调递增函数.

 ,单调递减区间为
,单调递减区间为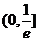 .……………………2分
.……………………2分 …………………………………………1分
…………………………………………1分 时,有
时,有 ,
,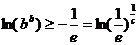 .
.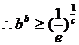 .……………………………………………………………………3分
.……………………………………………………………………3分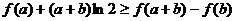 变形,得
变形,得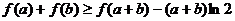 ,
,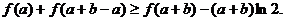
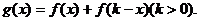 ……………………………………3分
……………………………………3分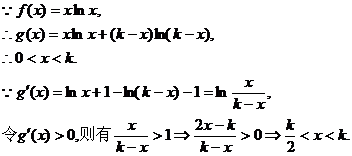
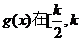 )上单调递增,在
)上单调递增,在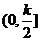 上单调递减.
上单调递减.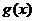 的最小值为
的最小值为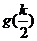 ,即总有
,即总有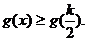
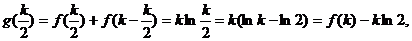


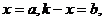 则
则
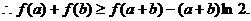
 ……………………………………4分
……………………………………4分