日照实验高中2007年高考一轮复习周测八
时间 120分钟 满分 150分
一、选择题
1、若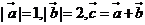 ,且
,且 ,则向量
,则向量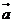 与
与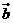 的夹角为C
的夹角为C
A 30° B 60° C 120° D 150°
2、已知函数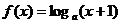 的定义域和值域都是[0,1],则
的定义域和值域都是[0,1],则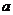 的值为
的值为
A 2
B 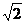 C
C 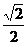 D
D 
3、下列各式中,值为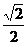 的是( )
的是( )
A
 B
B 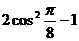
C 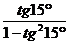 D
D 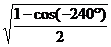
4、已知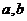 为实数,集合
为实数,集合 ,
,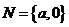 ,
,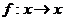 表示把
表示把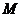 中的元素
中的元素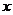 映射到集合
映射到集合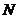 中仍为
中仍为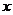 ,则
,则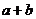 等于( C )
等于( C )
A 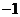 B
B  C
C 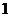 D
D 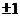
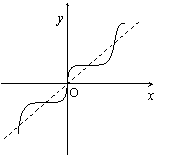 5、函数
5、函数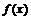 的部分图象如右图所示,则
的部分图象如右图所示,则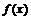 的解析式可能是( B )
的解析式可能是( B )
A.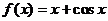 B.
B.
C.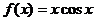 D.
D.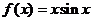
6、已知向量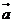 ≠
≠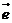 ,|
,|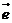 |=1,对任意t∈R,恒有|
|=1,对任意t∈R,恒有|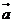 -t
-t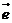 |≥|
|≥|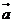 -
-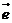 |,则 C
|,则 C
A 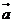 ⊥
⊥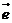 B
B 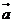 ⊥(
⊥(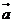 -
-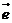 ) C
) C 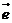 ⊥(
⊥(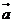 -
-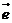 ) D (
) D (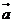 +
+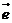 )⊥(
)⊥(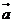 -
-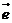 )
)
7、若函数f(x)
= + 2x + log2x的值域是
{3, -1,
5 + , 20},则其定义域是( B
)
A. {0,1,2,4} B. {,1,2,4} C. {,2,4} D. {,1,2,4,8}
8、已知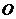 是四边形
是四边形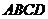 所在平面内的一点,且满足
所在平面内的一点,且满足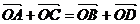 ,则四边形
,则四边形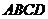 是A
是A
A 平行四边形 B 菱形 C 梯形 D 等腰梯形
班级____________ 姓名____________ 得分_______________
9、已知向量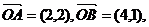 在
在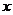 轴上的一点
轴上的一点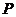 使
使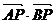 最小,则
最小,则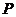 点坐标是
点坐标是
A (-3,0) B (2,0) C (3,0) D (4,0)
10、在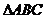 中,
中,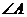 、
、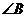 、
、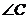 所对边的边长分别为
所对边的边长分别为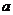 、
、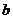 、
、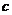 ,
,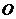 为
为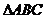 内一点,且满足
内一点,且满足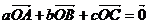 ,则
,则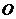 为
为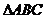 的( D
)
的( D
)
A 重心 B 外心 C 垂心 D 内心
11、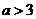 ,则方程
,则方程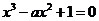 在(0,2)上恰好有 ( B )
在(0,2)上恰好有 ( B )
A. 0 个根 B. 1个根 C.2个根 D. 3个根
12、设函数f (x)的定义域为D,如果对于任意的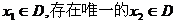 ,使
,使
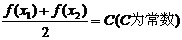 成立,则称函数f (x)在D上均值为C,给出下列四个函数
成立,则称函数f (x)在D上均值为C,给出下列四个函数
①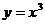 ②
②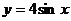 ③
③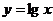 ④
④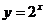
则满足在其定义域上均值为2的所有函数是( D )
A ①② B ③④ C ②④ D ①③
 二、填空题
二、填空题
13、设向量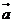 和
和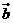 满足
满足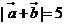 ,
,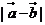 =3,则
=3,则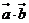 =______4
=______4
14、定义在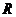 上的可导函数
上的可导函数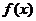 ,已知
,已知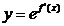 的图象
的图象
如右图所示,则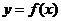 的递增区间是___________
的递增区间是___________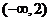
15、若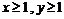 ,且
,且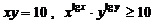 ,则
,则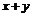 的值是 11
的值是 11
16、给出下列命题:①“p且q”为真是“p或q”为真的充分不必要条件;②“p且q”为假是“p或q”为假的充分不必要条件;③“p或q”为真是“Øp”为假的必要不充分条件;④“Øp”为真是“p且q”为假的必要不充分条件.其中正确命题的序号为________.
选择题答题卡
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
三、解答题
17、设集合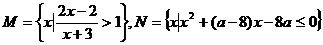 ,命题
,命题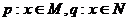
(1)当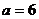 时,判断命题
时,判断命题 是命题
是命题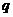 的什么条件;
的什么条件;
(2)求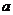 的取值范围,使命题
的取值范围,使命题 是命题
是命题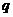 的必要不充分条件.
的必要不充分条件.
18、已知向量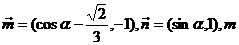 与
与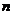 为共线向量,且
为共线向量,且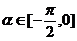
(Ⅰ)求 的值
的值
(Ⅱ)求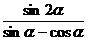 的值
的值
(Ⅰ)∵m与n为共线向量,∴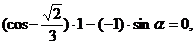
即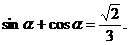
(Ⅱ)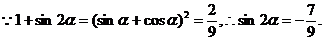
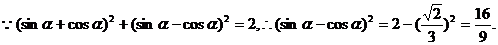
又
因此,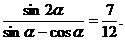
19、已知向量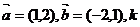 、
、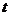 为正实数,
为正实数,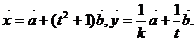
(1)若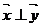 ,求k的最大值;
,求k的最大值;
(2)是否存在k、t使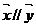 ?若存在,求出k的取值范围;若不存在,请说明理由.
?若存在,求出k的取值范围;若不存在,请说明理由.
解: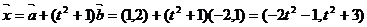 ,
,
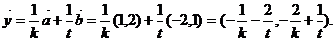 2分
2分
(1)若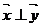 ,则
,则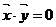 ,
,
即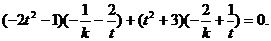 4分
4分
整理,得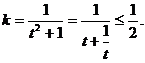
当且仅当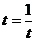 ,即t=1时,“=”成立.
,即t=1时,“=”成立. 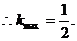 8分
8分
(2)假设存在正实数k、t,使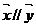 ,则
,则
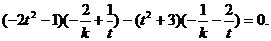 10分
10分
化简,得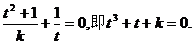 12分
12分
 k、t是正实数,故满足上式的k、t不存在.
k、t是正实数,故满足上式的k、t不存在.
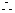 不存在这样的正实数k、t,使
不存在这样的正实数k、t,使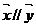 .
14分
.
14分
21、函数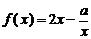 的定义域为
的定义域为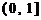 (
(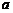 为实数).
为实数).
(1)当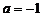 时,求函数
时,求函数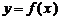 的值域;
的值域;
(2)若函数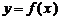 在定义域上是减函数,求
在定义域上是减函数,求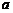 的取值范围;
的取值范围;
(3)函数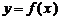 在
在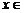
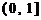 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时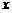 的值.
的值.
解:(1)显然函数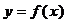 的值域为
的值域为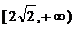 ; ……………3分
; ……………3分
(2)若函数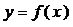 在定义域上是减函数,则任取
在定义域上是减函数,则任取
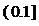 且
且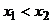 都有
都有 成立, 即
成立, 即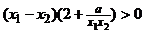
只要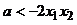 即可,
…………………………5分
即可,
…………………………5分
由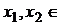
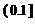 ,故
,故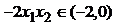 ,所以
,所以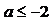 ,
,
故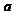 的取值范围是
的取值范围是 ;
…………………………7分
;
…………………………7分
(3)当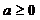 时,函数
时,函数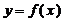 在
在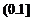 上单调增,无最小值,
上单调增,无最小值,
当 时取得最大值
时取得最大值 ;
;
由(2)得当 时,函数
时,函数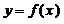 在
在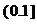 上单调减,无最大值,
上单调减,无最大值,
当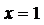 时取得最小值
时取得最小值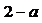 ;
;
当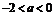 时,函数
时,函数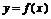 在
在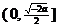 上单调减,在
上单调减,在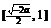 上单调增,无最大值,
上单调增,无最大值,
当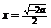 时取得最小值
时取得最小值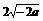 .
…………………………12分
.
…………………………12分
22、已知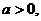 函数
函数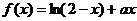
(I)设曲线 在点(1,f(1))处的切线为l,若l与圆(x+1)2+y2=1相切,求a的值;
在点(1,f(1))处的切线为l,若l与圆(x+1)2+y2=1相切,求a的值;
(II)求函数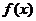 的单调区间;
的单调区间;
(III)求函数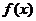 在[0,1]上的最小值.
在[0,1]上的最小值.
解:(I)依题意有, ,过
,过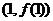 点的直线的斜率为
点的直线的斜率为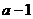 ,所以,过
,所以,过 点的直线方程为
点的直线方程为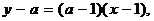
又已知圆圆心为(-1,0)半径为1,依题意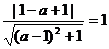 ,解之得
,解之得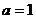 .
.
(II)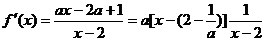
 ,
,
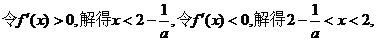 ………………6分
………………6分
所以,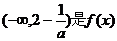 的增区间;
的增区间; 是
是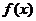 的减区间。…………7分
的减区间。…………7分
(III)当 即0<a≤
即0<a≤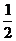 时,f(x)在[0,1]上是减函数,所以f(x)的最小值为f(1)=a,
时,f(x)在[0,1]上是减函数,所以f(x)的最小值为f(1)=a,
当0<2-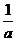 <1,
<1,
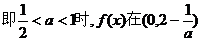 上是增函数,在
上是增函数,在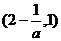 上是减函数,所以,需比较
上是减函数,所以,需比较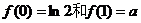 两个值的大小,
两个值的大小,
因为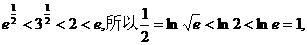 ………………10分
………………10分
∴当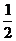 <a<lin2时,最小值为a,当lin2≤a<1时,最小值为lin2,
<a<lin2时,最小值为a,当lin2≤a<1时,最小值为lin2,
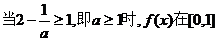 上是增函数,所以最小值为
上是增函数,所以最小值为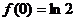 .……13分
.……13分
综上,当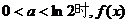 的最小值为a,当
的最小值为a,当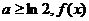 的最小值为
的最小值为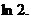 …14分
…14分