摘要：(2)是否存在k.t使?若存在.求出k的取值范围,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu_id_20950[举报]
在平面直角坐标系中，已知向量
=(c，0)(c为常数，且c＞0)，
=(x，x)(x∈R)，|
|的最小值为1，
=(
，t）（a为常数，且a＞c，t∈R）．动点P同时满足下列三个条件：
（1）|
|=
|
|；(2)
=λ•
(λ∈R，且λ≠0)；
（2）动点P的轨迹C经过点B（0，-1）．
（Ⅰ）求曲线C的方程；
（Ⅱ）是否存在方向向量为m=（1，k）（k≠0）的直线l，l与曲线C相交于M、N两点，使|
|=|
|，且
与
的夹角为60°？若存在，求出k值，并写出直线l的方程；若不存在，请说明理由．
查看习题详情和答案>>
| OF |
| OG |
| FG |
| OE |
| a2 |
| C |
（1）|
| PF |
| c |
| a |
| PE |
| PE |
| OF |
（2）动点P的轨迹C经过点B（0，-1）．
（Ⅰ）求曲线C的方程；
（Ⅱ）是否存在方向向量为m=（1，k）（k≠0）的直线l，l与曲线C相交于M、N两点，使|
| BM |
| BN |
| BM |
| BN |
对于给定数列{cn}，如果存在实常数p、q，使得cn+1＝pcn＋q对于任意n∈N*都成立，我们称数列{cn}是“k类数列”．
(Ⅰ)若an＝2n，bn＝3·2n，n∈N*，数列{an}、{bn}是否为“k类数列”？若是，指出它对应的实常数p、q，若不是，请说明理由；
(Ⅱ)证明：若数列{an}是“k类数列”，则数列{an＋an+1}也是“k类数列”；
(Ⅲ)若数列{an}满足a1＝2，an＋an+1＝3t·2n(n∈N*)，t为常数．求数列{an}前2012项的和．并判断{an}是否为“k类数列”，说明理由．
（2006•朝阳区三模）在平面直角坐标系中，已知向量
=（c，0）（c为常数，且c＞0），
=（x，x）（x∈R），
|
|的最小值为 1 ，
=(
， t)（a为常数，且a＞c，t∈R）．动点P同时满足下列三个条件：（1）|
|=
|
|；（2）
=λ
（λ∈R，且λ≠0）；（3）动点P的轨迹C经过点B（0，-1）．
（Ⅰ）求曲线C的方程；
（Ⅱ）是否存在方向向量为
=（1，k）（k≠0）的直线l，l与曲线C相交于M、N两点，使|
|=|
|，且
与
的夹角为60°？若存在，求出k值，并写出直线l的方程；若不存在，请说明理由．
查看习题详情和答案>>
| OF |
| OG |
|
| FG |
| OE |
| a2 |
| c |
| PF |
| c |
| a |
| PE |
| PE |
| OF |
（Ⅰ）求曲线C的方程；
（Ⅱ）是否存在方向向量为
| m |
| BM |
| BN |
| BM |
| BN |
，
，|
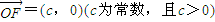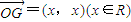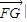的最小值为1，
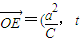）（a为常数，且a＞c，t∈R）．动点P同时满足下列三个条件：
•
；
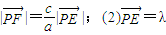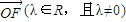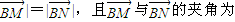60°？若存在，求出k值，并写出直线l的方程；若不存在，请说明理由．