摘要：(I)设曲线在点(1.f(1))处的切线为l.若l与圆(x+1)2+y2=1相切.求a的值,
网址：http://m.1010jiajiao.com/timu_id_20978[举报]
已知曲线f（x）=ax+blnx-1在点（1，f（1））处的切线为直线y=0．
（1）求实数a，b的值；
（2）设函数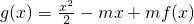
，其中m为常数．
（i）求g（x）的单调递增区间；
（ii）求证：当1＜m＜3，x∈（1，e）（其中e=2.71828…）时，总有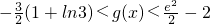
成立．
查看习题详情和答案>>
已知曲线f（x）=ax+blnx-1在点（1，f（1））处的切线为直线y=0．
（1）求实数a，b的值；
（2）设函数
，其中m为常数．
（i）求g（x）的单调递增区间；
（ii）求证：当1＜m＜3，x∈（1，e）（其中e=2.71828…）时，总有
成立．
查看习题详情和答案>>
（1）求实数a，b的值；
（2）设函数
，其中m为常数．（i）求g（x）的单调递增区间；
（ii）求证：当1＜m＜3，x∈（1，e）（其中e=2.71828…）时，总有
成立．查看习题详情和答案>>
（2013•天津）设a∈[-2，0]，已知函数f(x)=
（Ⅰ） 证明f（x）在区间（-1，1）内单调递减，在区间（1，+∞）内单调递增；
（Ⅱ） 设曲线y=f（x）在点Pi（xi，f（xi））（i=1，2，3）处的切线相互平行，且x1x2x3≠0，证明x1+x2+x3＞-
．
查看习题详情和答案>>
|
（Ⅰ） 证明f（x）在区间（-1，1）内单调递减，在区间（1，+∞）内单调递增；
（Ⅱ） 设曲线y=f（x）在点Pi（xi，f（xi））（i=1，2，3）处的切线相互平行，且x1x2x3≠0，证明x1+x2+x3＞-
| 1 |
| 3 |
．
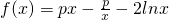，若在[1，e]上至少存在一点x0，使得f（x0）＞g（x0）成立，求实数p的取值范围．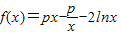
．
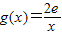，若在[1，e]上至少存在一点x，使得f（x）＞g（x）成立，求实数p的取值范围．