-
1.有同寝室的四位同学分别写一张贺年卡,先集中起来,然后每人去拿一张,设自己拿到自己写的贺卡的人数为
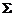 ,①求
,①求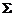 的概率分布;②求
的概率分布;②求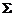 的数学期望与方差.
的数学期望与方差. -
2.有3张形状、大小、质量完全相同的卡片,在各张卡片上分别标上0、1、2。现从这3张卡片中任意抽出一张,读出其标号
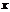 ,然后把这张卡片放回去,再抽一张,其标号为
,然后把这张卡片放回去,再抽一张,其标号为 ,记
,记 .(1)求
.(1)求 的分布列;(2)求
的分布列;(2)求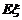 和
和 .
. -
3.甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次为ξ;乙用这枚硬币掷2次,记正面朝上的次为η.
(1)分别求ξ和η的期望;
(2)规定;若ξ>η,则甲获胜,若ξ<η,则乙获胜,分别求出甲和乙获胜的概率.
-
4.甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数
 的数学期望和方差.
的数学期望和方差. -
5.口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为
 .
.(Ⅰ)
 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;(Ⅱ)求随机变量
 的期望E
的期望E .
. -
6.A有一只放有x个红球,y个白球,z个黄球的箱子(x、y、z≥0,
且
 ),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.(1)用x、y、z表示B胜的概率;
(2)当A如何调整箱子中球时,才能使自己获胜的概率最大?
-
7.某中学有5名体育类考生要到某大学参加体育专业测试,学校指派一名教师带队,已知每位考生测试合格的概率都是
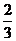 ,
,(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;
(2)若5人中恰有r人合格的概率为
 ,求r的值;
,求r的值;(3)记测试合格的人数为
 ,求
,求 的期望和方差.
的期望和方差. -
8.袋中有1个白球和4个黑球,每次从其中任取一个球,直到取到白球为止.
(Ⅰ)当每次取出的黑球不再放回时,求取球次数的数学期望与方差;
(Ⅱ)当每次取出的黑球仍放回去时,求取球次数的数学期望与方差.
-
9.从分别写有
 的九张卡片中,任意抽取两张,计算:
的九张卡片中,任意抽取两张,计算:(Ⅰ)卡片上的数字都是奇数的概率;
(Ⅱ)当两张卡片上的数字之和能被3整除时,就说这次试验成功,求在15次试验中成功次数
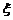 的数学期望.
的数学期望. -
10.甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格。
(Ⅰ)求甲答对试题数
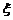 的概率分布及数学期望,
的概率分布及数学期望,(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
-
11.学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设
 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且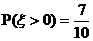 .(I) 求文娱队的人数;(II) 写出
.(I) 求文娱队的人数;(II) 写出 的概率分布列并计算
的概率分布列并计算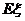 .
. -
12.某中学篮球队进行投篮训练,每人在一轮练习中最多可投篮4次,现规定一旦命中即停止该轮练习,否则一直投到4次为止.已知运动员甲的投篮命中率为0.7.
(1) 求一轮练习中运动员甲的投篮次数ξ的分布列,并求出ξ的期望Eξ(结果保留两位有效数字);
(2) 求一轮练习中运动员甲至少投篮3次的概率.
-
13.甲、乙两名射击运动员,甲射击一次命中10环的概率为
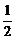 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ= ,
,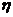 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.(1)求s的值及
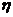 的分布列, (2)求
的分布列, (2)求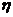 的数学期望.
的数学期望.概率解答题练习
-
1.有同寝室的四位同学分别写一张贺年卡,先集中起来,然后每人去拿一张,设自己拿到自己写的贺卡的人数为
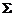 ,①求
,①求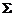 的概率分布;②求
的概率分布;②求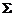 的数学期望与方差.
的数学期望与方差. -
1.解:(1)分布列
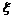
0
1
2
4


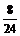

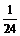
(2)
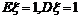 .
. -
2.有3张形状、大小、质量完全相同的卡片,在各张卡片上分别标上0、1、2。现从这3张卡片中任意抽出一张,读出其标号
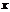 ,然后把这张卡片放回去,再抽一张,其标号为
,然后把这张卡片放回去,再抽一张,其标号为 ,记
,记 。(1)求
。(1)求 的分布列;(2)求
的分布列;(2)求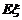 和
和 。
。解:(1)
 可能取的值为0、1、2、4。
……(2分)
可能取的值为0、1、2、4。
……(2分)且
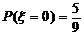 ,
,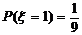 ,
,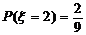 ,
, ……(6分)
……(6分) 所求的分布列为:
所求的分布列为:

0
1
2
4
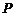
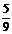

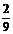

……(8分)
(2)由(1)可知,
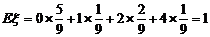 ……(11分)
……(11分)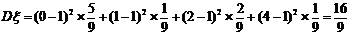 ……(14分)
……(14分) -
3.(本题满分14分)甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次为ξ;乙用这枚硬币掷2次,记正面朝上的次为η.
(1)分别求ξ和η的期望;
(2)规定;若ξ>η,则甲获胜,若ξ<η,则乙获胜,分别求出甲和乙获胜的概率.
解
 ξ的可能取值为0,1,2,3则ξ的分布列为
ξ的可能取值为0,1,2,3则ξ的分布列为ξ
0
1
2
3
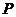

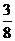
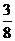

则Eξ
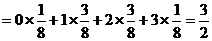
η的可能取值为0,1,2则η的分布列为
η
0
1
2
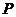
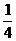


则Eη=
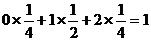
所以ξ、η的数学期望分别为
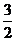 、1
、1(2)P(ξ>η)=
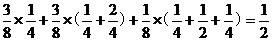
P(ξ<η)=

所以甲获胜的概率为
 ,乙获胜的概率为
,乙获胜的概率为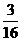 。
。 -
4.甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数
 的数学期望和方差.
的数学期望和方差.解:(1)记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1,乙为P2.(2分)
则P(A)=P1=0.6,P(B)=P2
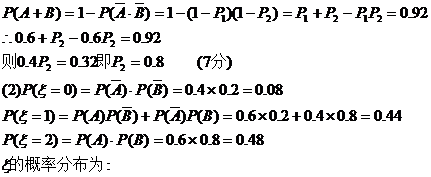

0
1
2
P
0.08
0.44
0.48
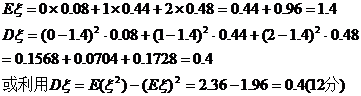
-
5.口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为
 .
.(Ⅰ)
 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;(Ⅱ)求随机变量
 的期望E
的期望E 。
。解(I)依题意,随机变量
 的取值是2、3、4、5、6…………2分
的取值是2、3、4、5、6…………2分因为P(
 =2)=
=2)= ;P(
;P( =3)=
=3)=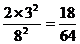
P(
 =4)=
=4)=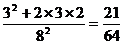 ;P(
;P( =5)=
=5)= ;
;P(
 =6)=
=6)=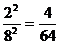 ;…………7分
;…………7分所以,当
 =4时,其发生的概率P(
=4时,其发生的概率P( =4)=
=4)=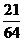 最大…………8分
最大…………8分(Ⅱ)E
 =
=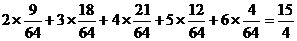 ………………12分
………………12分 -
6.(本小题满分12分)A有一只放有x个红球,y个白球,z个黄球的箱子(x、y、z≥0,
且
 ),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.(1)用x、y、z表示B胜的概率;
(2)当A如何调整箱子中球时,才能使自己获胜的概率最大?
解:(1)显然A胜与B胜为对立事件,A胜分为三个基本事件:
①A1:“A、B均取红球”;②A2:“A、B均取白球”;③A3:“A、B均取黄球”.
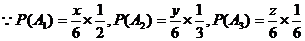
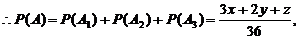
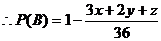
(2)由(1)知
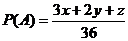 ,
,
于是
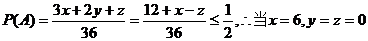 ,即A在箱中只放6
,即A在箱中只放6个红球时,获胜概率最大,其值为
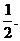
-
7.某中学有5名体育类考生要到某大学参加体育专业测试,学校指派一名教师带队,已知每位考生测试合格的概率都是
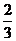 ,
,(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;
(2)若5人中恰有r人合格的概率为
 ,求r的值;
,求r的值;(3)记测试合格的人数为
 ,求
,求 的期望和方差。
的期望和方差。解:(1)体育教师不坐后排记为事件A,则
 。
。(2)每位考生测试合格的概率
 ,测试不合格的概率为
,测试不合格的概率为
则
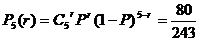 ,即
,即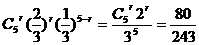 ,
,∴
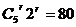 ,
,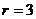
(3)∵
 -
-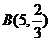
∴
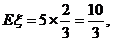
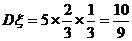
-
8.袋中有1个白球和4个黑球,每次从其中任取一个球,直到取到白球为止.
(Ⅰ)当每次取出的黑球不再放回时,求取球次数的数学期望与方差;
(Ⅱ)当每次取出的黑球仍放回去时,求取球次数的数学期望与方差。
解(Ⅰ)当每次取出的黑球不再放回时,设随机变量
 是取球次数,因为每次取出的黑球不再放回,所以
是取球次数,因为每次取出的黑球不再放回,所以 的可能取值为1,2,3,4,5,易知
的可能取值为1,2,3,4,5,易知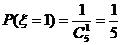
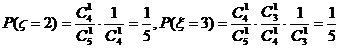 ,
,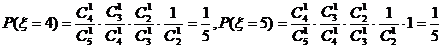 ,
,故随机变量
 的概率分布列为:
的概率分布列为:
1
2
3
4
5
P
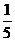
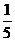
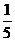
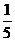
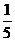
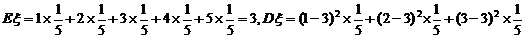
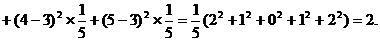 …………….6分
…………….6分(Ⅱ)当每次取出的黑球仍放回去时,设随机变量
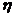 是取球次数,因为每次取出的黑球仍放回去,所以
是取球次数,因为每次取出的黑球仍放回去,所以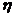 的可能取值是一切正整数,
的可能取值是一切正整数,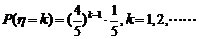
所求概率分布为
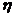
1
2
3
…
n
…
P
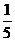
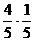
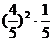
…
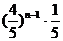
…
-
9.从分别写有
 的九张卡片中,任意抽取两张,计算:
的九张卡片中,任意抽取两张,计算:(Ⅰ)卡片上的数字都是奇数的概率;
(Ⅱ)当两张卡片上的数字之和能被3整除时,就说这次试验成功,求在15次试验中
成功次数
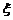 的数学期望。
的数学期望。(Ⅰ)
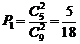 ;
;(Ⅱ)一次试验成功的概率为
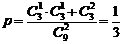 ,从而
,从而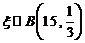 ,故
,故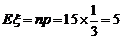 。
。 -
10.甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格。
(Ⅰ)求甲答对试题数
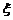 的概率分布及数学期望。
的概率分布及数学期望。(Ⅱ)求甲、乙两人至少有一人考试合格的概率。
解:(Ⅰ)依题意,甲答对试题数
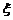 的概率分布如下:
的概率分布如下: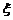
0
1
2
3
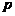

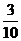

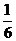
…………4分
甲答对试题数
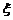 的数学期望:
的数学期望: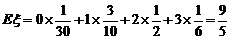 ……………………………………4分
……………………………………4分(Ⅱ)设甲、乙两人考试合格的事件分别为
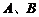
则
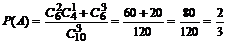
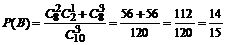 …………………理9分(文6分)
…………………理9分(文6分)甲、乙两人考试均不合格的概率为:
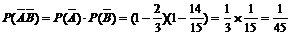
∴甲、乙两人至少一个合格的概率为
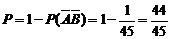 ………理文均12分
………理文均12分 -
11.学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设
 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且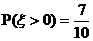 .
.(I) 求文娱队的人数;
(II) 写出
 的概率分布列并计算
的概率分布列并计算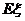 .
.解:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是
(7-2 x)人.
(I)∵
 ,
,∴
 .……………………………………3分
.……………………………………3分即
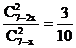 .
.∴
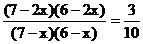 .
.∴x=2. ……………………………………5分
故文娱队共有5人.……………………………………7分
(II)
 的概率分布列为
的概率分布列为
0
1
2
P
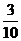


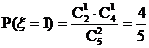 ,……………………………………9分
,……………………………………9分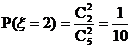 ,……………………………………11分
,……………………………………11分∴
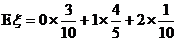 =1.
…………………………13分
=1.
…………………………13分 -
12.某中学篮球队进行投篮训练,每人在一轮练习中最多可投篮4次,现规定一旦命中即停止该轮练习,否则一直投到4次为止.已知运动员甲的投篮命中率为0.7.
(3) 求一轮练习中运动员甲的投篮次数ξ的分布列,并求出ξ的期望Eξ(结果保留两位有效数字);
(4) 求一轮练习中运动员甲至少投篮3次的概率.
解:(1)ξ的可能取值为1,2,3,4,
ξ=1时,P(ξ=1)=0.7
ξ=2时,P(ξ=2)=0.7(1-0.7)=0.21;
ξ=3时,P(ξ=3)=0.7(1-0.7)2=0.063
ξ=4时,P(ξ=4)=0.7(1-0.7)3+(1-0.7)4=0.027.
∴ξ的分布为
ξ
1
2
3
4
P
0.7
0.21
0.063
0.027
∴Eξ=1×0.7+×2×0.21+3×0.063+4×0.027=1.4
(2)P(ξ≥3)=P(ξ=3)+P(ξ=4)=0.063+0027=0.09
-
13.甲、乙两名射击运动员,甲射击一次命中10环的概率为
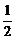 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ= ,
,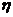 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.(1)求s的值及
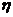 的分布列,
的分布列,(2)求
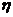 的数学期望.
的数学期望.解:(1)依题意知ξ∽B(2,s),故Eξ=2s=
 ,
,∴s=
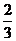 .
…………2分
.
…………2分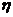 的取值可以是0,1,2.
的取值可以是0,1,2.甲、乙两人命中10环的次数均为0次的概率是
 ,
,甲、乙两人命中10环的次数均为1次的概率是
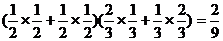 ,
,甲、乙两人命中10环的次数均为2次的概率是
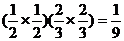 ,
,∴
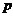 (
(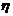 =0)=
=0)=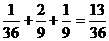 .
…………6分
.
…………6分甲命中10环的次数为2次且乙命中10环的次数为0次的概率是
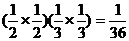 ,
,甲命中10环的次数为0次且乙命中10环的次数为2次的概率是
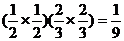 .
.∴
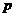 (
(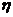 =2)=
=2)=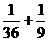 =
=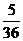 ,
,
∴
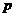 (
(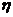 =1)=1
=1)=1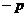 (
(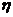 =0)
=0)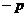 (
(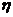 =2)=
=2)= . ………10分
. ………10分故
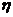 的分布列是
的分布列是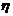
0
1
2
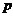
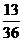

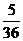
………12分
(2)E
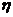 =
=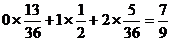 .
…………14分
.
…………14分