-
1.(全国Ⅰ•理•7题)如图,正四棱柱
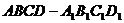 中,
中,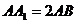 ,则异面直线
,则异面直线 所成角的余弦值为( D )
所成角的余弦值为( D )A.
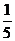 B.
B. C.
C.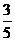 D.
D.
-
2.(全国Ⅱ•理•7题)已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦等于( A )
A.
 B.
B.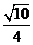 C.
C. D.
D.
-
3.(北京•理•3题)平面
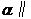 平面
平面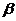 的一个充分条件是( D )
的一个充分条件是( D )A.存在一条直线
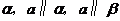 B.存在一条直线
B.存在一条直线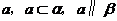
C.存在两条平行直线

D.存在两条异面直线

-
4.(安徽•理•2题)设
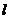 ,
, ,
, 均为直线,其中
均为直线,其中 ,
, 在平面
在平面 内,“
内,“ ”是
”是 且“
且“ ”的( )
”的( )A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
-
5.(安徽•理•8题)半径为1的球面上的四点
 是正四面体的顶点,则
是正四面体的顶点,则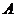 与
与 两点间的球面距离为( )
两点间的球面距离为( )A.
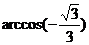 B.
B.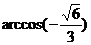 C.
C. D.
D.
-
6.(福建•理•8题)已知
 ,
, 为两条不同的直线,
为两条不同的直线, ,
,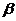 为两个不同的平面,则下列命题中正确的是( D )
为两个不同的平面,则下列命题中正确的是( D )A .
 B.
B. 
C.
 D.
D. 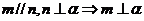
-
7.(福建•理•10题)顶点在同一球面上的正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=
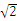 ,则A、C两点间的球面距离为( B )
,则A、C两点间的球面距离为( B )A .
 B.
B.
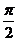 C .
C .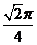 D.
D. 
-
8.(湖北•理•4题)平面
 外有两条直线
外有两条直线 和
和 ,如果
,如果 和
和 在平面
在平面 内的射影分别是
内的射影分别是 和
和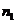 ,给出下列四个命题:
,给出下列四个命题:①
 ⊥
⊥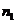

 ⊥
⊥ ;
②
;
② ⊥
⊥

 ⊥
⊥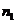 ;
;③
 与
与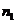 相交
相交
 与
与 相交或重合;
④
相交或重合;
④ 与
与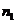 平行
平行
 与
与 平行或重合;
平行或重合;其中不正确的命题个数是( D )
A.1 B.2 C.3 D.4
-
9.(湖南•理•8题)棱长为1的正方体
 的8个顶点都在球
的8个顶点都在球 的表面上,
的表面上,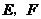 分别是棱
分别是棱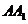 ,
, 的中点,则直线
的中点,则直线 被球
被球 截得的线段长为(
D )
截得的线段长为(
D )A.
 B.
B. C.
C. D.
D.
-
10.(江苏•理•4题)已知两条直线
 ,两个平面
,两个平面 ,给出下面四个命题:
,给出下面四个命题:①
 ②
②
③
 ④
④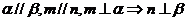
 其中正确命题的序号是( C )
其中正确命题的序号是( C )A.①③ B.②④ C.①④ D.②③
-
11.(江西•理•7题)如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,错误的命题是( D )
A.点H是△A1BD的垂心 B.AH垂直平面CB1D1
C.AH的延长线经过点C1 D.直线AH和BB1所成角为45°
-
12.(辽宁•理•7题)若
 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )A.若
 ,则
,则 B.若
B.若
 ,
, ,则
,则
C.若
 ,
, ,则
,则 D.若
D.若 ,
, ,则
,则
-
13.
 (陕西•理•6题)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( B )
(陕西•理•6题)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( B )A.
 B.
B. C.
C.  D.
D.
-
14.(四川•理•4题)如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( D )
A.BD∥平面CB1D1 B.AC1⊥BD
C.AC1⊥平面CB1D1 D.异面直线AD与CB1角为60°
-
15.
 (宁夏•理•8题) 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( B )
(宁夏•理•8题) 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( B )A.
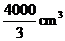 B.
B. C.
C.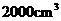 D.
D.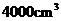
-
16.
 (四川•理•6题)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是
(四川•理•6题)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是 ,且三面角B-OA-C的大小为
,且三面角B-OA-C的大小为 ,则从A点沿球面经B、C两点再回到A点的最短距离是( C )
,则从A点沿球面经B、C两点再回到A点的最短距离是( C )A.
 B.
B. C.
C. D.
D.
-
17.(天津•理•6题)设
 为两条直线,
为两条直线, 为两个平面,下列四个命题中,正确的命题是( D )
为两个平面,下列四个命题中,正确的命题是( D )A.若
 与
与 所成的角相等,则
所成的角相等,则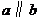 B.若
B.若 ,
, ,则
,则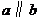
C.若
 ,则
,则 D.若
D.若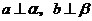 ,
, ,则
,则
-
18.(浙江•理•6题)若P是两条异面直线
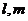 外的任意一点,则(
B )
外的任意一点,则(
B )A.过点P有且仅有一条直线与
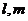 都平行
B.过点P有且仅有一条直线与
都平行
B.过点P有且仅有一条直线与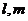 都垂直
都垂直C.过点P有且仅有一条直线与
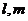 都相交
D.过点P有且仅有一条直线与
都相交
D.过点P有且仅有一条直线与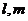 都异面
都异面 -
19.(全国Ⅰ•理•16题)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上。已知正三棱柱的底面边长为2,则该三角形的斜边长为
 。
。 -
20.(全国Ⅱ•理•15题)一个正四棱柱的各个顶点在一个直径为2cm的球面上。如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为
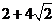 cm2。
cm2。 -
21.(安徽•理•15题)在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号)。
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体。
-
22.(江苏•理•14题)正三棱锥
 高为2,侧棱与底面所成角为
高为2,侧棱与底面所成角为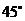 ,则点
,则点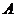 到侧面
到侧面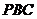 的距离是 .
的距离是 . -
23.(辽宁•理•15题)若一个底面边长为
 ,棱长为
,棱长为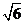 的正六棱柱的所有顶点都在一个平面上,则此球的体积为
.
的正六棱柱的所有顶点都在一个平面上,则此球的体积为
. -
24.
 (上海•理•10题)平面内两直线有三种位置关系:相交,平行与重合。已知两个相交平面
(上海•理•10题)平面内两直线有三种位置关系:相交,平行与重合。已知两个相交平面 与两直线
与两直线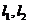 ,又知
,又知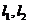 在
在 内的射影为
内的射影为 ,在
,在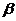 内的射影为
内的射影为 。试写出
。试写出 与
与 满足的条件,使之一定能成为
满足的条件,使之一定能成为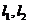 是异面直线的充分条件
是异面直线的充分条件  平行,
平行, 相交 。
相交 。 -
25.(四川•理•14题)如图,在正三棱柱ABC-A1B1C1中,侧棱长为
 ,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是
,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是 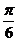 .
. -
26.(天津•理•12题)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为
 .
. -
27.(浙江•理•16题)已知点O在二面角
 的棱上,点P在
的棱上,点P在 内,且
内,且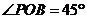 。若对于
。若对于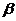 内异于O的任意一点Q,都有
内异于O的任意一点Q,都有 ,则二面角
,则二面角 的大小是____
的大小是____ ____。
____。 -
27.(全国Ⅰ•理•19题)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD。已知∠ABC=45°,AB=2,BC=2
 ,SA=SB=
,SA=SB= 。
。(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小;
解答:解法一:
(Ⅰ)作
 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面 底面
底面 ,得
,得 底面
底面 .
.因为
 ,所以
,所以 ,
,又
 ,故
,故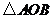 为等腰直角三角形,
为等腰直角三角形, ,
,由三垂线定理,得
 .
. (Ⅱ)由(Ⅰ)知
(Ⅱ)由(Ⅰ)知 ,依题设
,依题设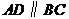 ,
,故
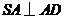 ,由
,由 ,
,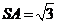 ,
, ,得
,得 ,
,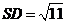 .
. 的面积
的面积 .
.连结
 ,得
,得 的面积
的面积
设
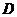 到平面
到平面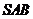 的距离为
的距离为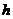 ,由于
,由于 ,得
,得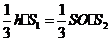 ,
,解得
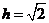 .
.设
 与平面
与平面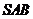 所成角为
所成角为 ,则
,则 .
.所以,直线
 与平面
与平面 所成的我为
所成的我为 .
.解法二:
(Ⅰ)作
 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面 底面
底面 ,得
,得 平面
平面 .
.因为
 ,所以
,所以 .
.又
 ,
,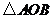 为等腰直角三角形,
为等腰直角三角形, .
. 如图,以
如图,以 为坐标原点,
为坐标原点, 为
为 轴正向,建立直角坐标系
轴正向,建立直角坐标系 ,
, ,
,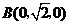 ,
,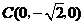 ,
, ,
, ,
,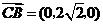 ,
, ,所以
,所以 .
.(Ⅱ)取
 中点
中点 ,
,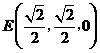 ,
,连结
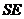 ,取
,取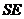 中点
中点 ,连结
,连结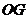 ,
, .
. ,
,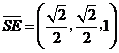 ,
,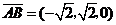 .
. ,
,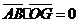 ,
,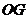 与平面
与平面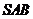 内两条相交直线
内两条相交直线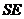 ,
, 垂直.
垂直.所以
 平面
平面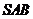 ,
, 与
与 的夹角记为
的夹角记为 ,
, 与平面
与平面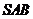 所成的角记为
所成的角记为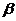 ,则
,则 与
与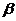 互余.
互余.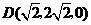 ,
, .
. ,
,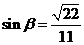 ,
,所以,直线
 与平面
与平面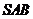 所成的角为
所成的角为 .
. -
28.(全国Ⅱ•理•19题)如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点。
 (Ⅰ)求证:EF∥平面SAD;(Ⅱ)设SD = 2CD,求二面角A-EF-D的大小;
(Ⅰ)求证:EF∥平面SAD;(Ⅱ)设SD = 2CD,求二面角A-EF-D的大小;解法一:
(1)作
 交
交 于点
于点 ,则
,则 为
为 的中点.
的中点.连结
 ,又
,又 ,
,故
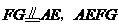 为平行四边形.
为平行四边形. ,又
,又 平面
平面 平面
平面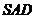 .
.所以
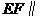 平面
平面 .
.(2)不妨设
 ,则
,则 为等
为等腰直角三角形.
取
 中点
中点 ,连结
,连结 ,则
,则 .
.又
 平面
平面 ,所以
,所以 ,而
,而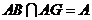 ,
,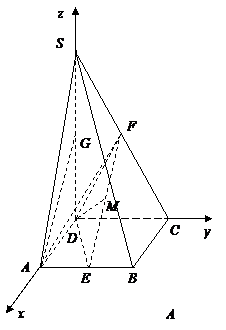 所以
所以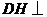 面
面 .
.取
 中点
中点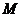 ,连结
,连结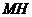 ,则
,则 .
.连结
 ,则
,则 .
.故
 为二面角
为二面角 的平面角
的平面角 .
.所以二面角
 的大小为
的大小为 .
.解法二:(1)如图,建立空间直角坐标系
 .
.设
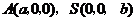 ,则
,则
 ,
,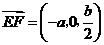 .
.取
 的中点
的中点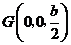 ,则
,则 .
. 平面
平面 平面
平面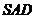 ,
,所以
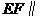 平面
平面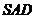 .
.(2)不妨设
 ,则
,则 .
. 中点
中点
 又
又 ,
,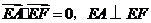 ,
,所以向量
 和
和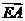 的夹角等于二面角
的夹角等于二面角 的平面角.
的平面角.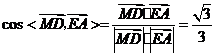 .
.所以二面角
 的大小为
的大小为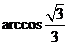 .
. -
29.(北京•理•16题)如图,在
 中,
中, ,斜边
,斜边 .
. 可以通过
可以通过 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角.动点
是直二面角.动点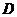 的斜边
的斜边 上.
上.(I)求证:平面
 平面
平面 ;
;(II)当
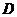 为
为 的中点时,求异面直线
的中点时,求异面直线 与
与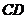 所成角的大小;
所成角的大小; (III)求
(III)求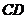 与平面
与平面 所成角的最大值.
所成角的最大值.解法一:
(I)由题意,
 ,
, ,
, 是二面角
是二面角 是直二面角,
是直二面角,又
 二面角
二面角 是直二面角,
是直二面角, ,又
,又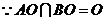 ,
,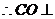 平面
平面 ,
,又
 平面
平面 .
. 平面
平面 平面
平面 .
.(II)作
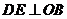 ,垂足为
,垂足为 ,连结
,连结 (如图),则
(如图),则 ,
, 是异面直线
是异面直线 与
与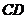 所成的角.
所成的角.在
 中,
中, ,
, ,
, .
.又
 .
. 在
在 中,
中, .
. 异面直线
异面直线 与
与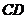 所成角的大小为
所成角的大小为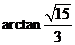 .
.(III)由(I)知,
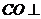 平面
平面 ,
, 是
是 与平面
与平面 所成的角,且
所成的角,且 .
.当
 最小时,
最小时, 最大,
最大,这时,
 ,垂足为
,垂足为 ,
, ,
, ,
,
 与平面
与平面 所成角的最大值为
所成角的最大值为 .
.解法二:
(I)同解法一.
(II)建立空间直角坐标系
 ,如图,则
,如图,则 ,
, ,
, ,
, ,
, ,
,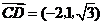 ,
,
 .
. 异面直线
异面直线 与
与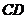 所成角的大小为
所成角的大小为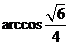 .
.(III)同解法一
-
30.
 (安徽•理•17题)如图,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2。
(安徽•理•17题)如图,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2。(Ⅰ)求证:A1C1与AC共面,B1D1与BD共面;
(Ⅱ)求证:平面A1ACC1⊥平面B1BDD1;
(Ⅲ)求二面角A-BB1-C的大小(用反三角函数值圾示);
-
31.(福建•理•18题)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。
(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)求点C到平面A1BD的距离;
分析:本小题主要考查直线与平面的位置关系,二面角的大小,点到平面的距离等知识,考查空间想象能力、逻辑思维能力和运算能力.满分12分.
解答:解法一:(Ⅰ)取
 中点
中点 ,连结
,连结 .
. 为正三角形,
为正三角形, .
.
 正三棱柱
正三棱柱 中,平面
中,平面 平面
平面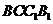 ,
,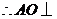 平面
平面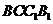 .
.连结
 ,在正方形
,在正方形 中,
中, 分别为
分别为 的中点,
的中点, ,
, .
.在正方形
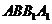 中,
中, ,
,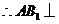 平面
平面 .
.(Ⅱ)设
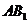 与
与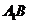 交于点
交于点 ,在平面
,在平面 中,作
中,作 于
于 ,连结
,连结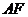 ,由(Ⅰ)得
,由(Ⅰ)得 平面
平面 .
. ,
,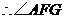 为二面角
为二面角 的平面角.
的平面角.在
 中,由等面积法可求得
中,由等面积法可求得 ,
,又
 ,
,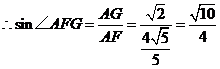 .
.所以二面角
 的大小为
的大小为 .
.(Ⅲ)
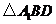 中,
中, ,
, .
.在正三棱柱中,
 到平面
到平面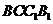 的距离为
的距离为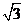 .
.设点
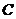 到平面
到平面 的距离为
的距离为 .
.由
 得
得 ,
,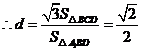 .
. 点
点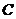 到平面
到平面 的距离为
的距离为 .
.解法二:(Ⅰ)取
 中点
中点 ,连结
,连结 .
. 为正三角形,
为正三角形, .
. 在正三棱柱
在正三棱柱 中,平面
中,平面 平面
平面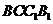 ,
, 平面
平面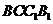 .
.取
 中点
中点 ,以
,以 为原点,
为原点,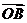 ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
,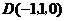 ,
, ,
, ,
,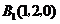 ,
, ,
, ,
, .
. ,
, ,
,
 ,
, .
.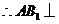 平面
平面 .
.(Ⅱ)设平面
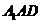 的法向量为
的法向量为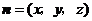 .
.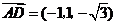 ,
, .
.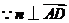 ,
, ,
,

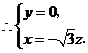
令
 得
得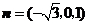 为平面
为平面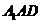 的一个法向量.
的一个法向量.由(Ⅰ)知
 平面
平面 ,
, 为平面
为平面 的法向量.
的法向量. ,
,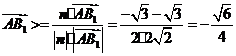 .
. 二面角
二面角 的大小为
的大小为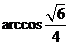 .
.(Ⅲ)由(Ⅱ),
 为平面
为平面 法向量,
法向量, .
. 点
点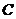 到平面
到平面 的距离
的距离 .
. -
32.(广东•理•19题)如图6所示,等腰△ABC的底边AB=6
 ,高CD=3,点B是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE。记BE=x,V(x)表示四棱锥P-ACFE的体积。
,高CD=3,点B是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE。记BE=x,V(x)表示四棱锥P-ACFE的体积。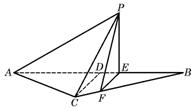 (Ⅰ)求V(x)的表达式;
(Ⅰ)求V(x)的表达式;(Ⅱ)当x为何值时,V(x)取得最大值?
(Ⅲ)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值;
-
33.
 (湖北•理•18题)如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
(湖北•理•18题)如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 。
。(Ⅰ)求证:平面VAB⊥平面VCD ;
(Ⅱ)当角θ变化时,求直线BC与平面VAB所成的角的取值范围;
分析:本小题主要考查线面关系、直线与平面所成角的有关知识,考查空间想象能力和推理运算能力以及应用向量知识解决数学问题的能力.
解答:解法1:(Ⅰ)
 ,
, 是等腰三角形,又
是等腰三角形,又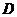 是
是 的中点,
的中点, ,又
,又 底面
底面 .
. .于是
.于是 平面
平面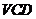 .
.又
 平面
平面 ,
, 平面
平面 平面
平面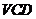 .
.(Ⅱ) 过点
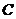 在平面
在平面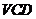 内作
内作 于
于 ,则由(Ⅰ)知
,则由(Ⅰ)知 平面
平面 .
.连接
 ,于是
,于是 就是直线
就是直线 与平面
与平面 所成的角.
所成的角. 在
在 中,
中, ;
;设
 ,在
,在 中,
中,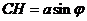 ,
, .
. ,
, ,
, .
.又
 ,
, .
.即直线
 与平面
与平面 所成角的取值范围为
所成角的取值范围为 .
.解法2:(Ⅰ)以
 所在的直线分别为
所在的直线分别为 轴、
轴、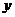 轴、
轴、 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则 ,
,于是,
 ,
, ,
,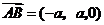 .
.从而
 ,即
,即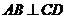 .
.同理
 ,
,即
 .又
.又 ,
, 平面
平面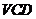 .
.又
 平面
平面 .
. 平面
平面 平面
平面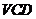 .
.(Ⅱ)设直线
 与平面
与平面 所成的角为
所成的角为 ,平面
,平面 的一个法向量为
的一个法向量为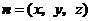 ,
, 则由
则由 .
.得

可取
 ,又
,又 ,
,于是
 ,
, ,
, ,
, .
.又
 ,
, .
.即直线
 与平面
与平面 所成角的取值范围为
所成角的取值范围为 .
.解法3:(Ⅰ)以点
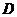 为原点,以
为原点,以 所在的直线分别为
所在的直线分别为 轴、
轴、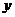 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则 ,
, ,于是
,于是 ,
, ,
, .
.从而
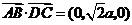
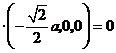 ,即
,即 .
.同理
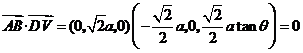 ,即
,即 .
.又
 ,
, 平面
平面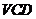 .
.又
 平面
平面 ,
, 平面
平面 平面
平面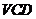 .
.(Ⅱ)设直线
 与平面
与平面 所成的角为
所成的角为 ,平面
,平面 的一个法向量为
的一个法向量为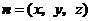 ,
, 则由
则由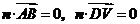 ,得
,得
可取
 ,又
,又 ,
,于是
 ,
, ,
, ,
, .
.又
 ,
, ,
,即直线
 与平面
与平面 所成角的取值范围为
所成角的取值范围为 .
.解法4:以
 所在直线分别为
所在直线分别为 轴、
轴、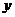 轴、
轴、 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则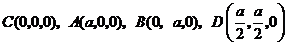 .设
.设 .
. (Ⅰ)
(Ⅰ) ,
, ,
,即
 .
.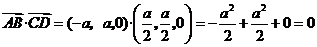 ,
,即
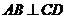 .
.又
 ,
, 平面
平面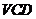 .
.又
 平面
平面 ,
, 平面
平面 平面
平面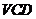 .
.(Ⅱ)设直线
 与平面
与平面 所成的角为
所成的角为 ,
,设
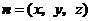 是平面
是平面 的一个非零法向量,
的一个非零法向量,则
 取
取 ,得
,得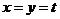 .
.可取
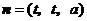 ,又
,又 ,
,于是
 ,
,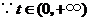 ,
, 关于
关于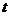 递增.
递增. ,
, .
.即直线
 与平面
与平面 所成角的取值范围为
所成角的取值范围为 .
. -
34.
 (湖南•理•18题)如图1,
(湖南•理•18题)如图1, 分别是矩形
分别是矩形 的边
的边 的中点,
的中点, 是
是 上的一点,将
上的一点,将 ,
, 分别沿
分别沿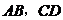 翻折成
翻折成 ,
, ,并连结
,并连结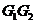 ,使得平面
,使得平面 平面
平面 ,
, ,且
,且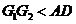 .连结
.连结 ,如图2.
,如图2. (I)证明:平面
 平面
平面 ;
;(II)当
 ,
, ,
,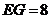 时,求直线
时,求直线 和平面
和平面 所成的角;
所成的角;解:解法一:(I)因为平面
 平面
平面 ,平面
,平面 平面
平面 ,
, ,
, 平面
平面 ,所以
,所以 平面
平面 ,又
,又 平面
平面 ,所以平面
,所以平面
 平面
平面 .
.(II)过点
 作
作 于点
于点 ,连结
,连结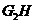 .
.由(I)的结论可知,
 平面
平面 ,
,所以
 是
是 和平面
和平面 所成的角.
所成的角.因为平面
 平面
平面 ,平面
,平面 平面
平面
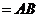 ,
, ,
, 平面
平面 ,所以
,所以 平面
平面 ,故
,故 .
.因为
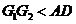 ,
, ,所以可在
,所以可在 上取一点
上取一点 ,使
,使 ,又因为
,又因为 ,所以四边形
,所以四边形 是矩形.
是矩形.由题设
 ,
, ,
,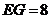 ,则
,则 .所以
.所以 ,
,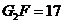 ,
, ,
, .
.因为
 平面
平面 ,
, ,所以
,所以 平面
平面 ,从而
,从而 .
.故
 ,
,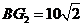 .
.又
 ,由
,由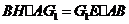 得
得 .
.故
 .
.即直线
 与平面
与平面 所成的角是
所成的角是 .
.解法二:(I)因为平面
 平面
平面 ,平面
,平面 平面
平面
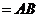 ,
, ,
, 平面
平面 ,所以
,所以 平面
平面 ,从而
,从而 .又
.又 ,所以
,所以 平面
平面 .因为
.因为 平面
平面 ,所以平面
,所以平面
 平面
平面 .
. (II)由(I)可知,
(II)由(I)可知, 平面
平面 .故可以
.故可以 为原点,分别以直线
为原点,分别以直线 为
为 轴、
轴、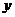 轴、
轴、 轴建立空间直角坐标系(如图),
轴建立空间直角坐标系(如图),由题设
 ,
, ,
,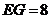 ,则
,则 ,
, ,
,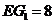 ,相关各点的坐标分别是
,相关各点的坐标分别是 ,
, ,
, ,
, .
.所以
 ,
, .
.设
 是平面
是平面 的一个法向量,
的一个法向量,由
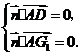 得
得 故可取
故可取 .
.过点
 作
作 平面
平面 于点
于点 ,因为
,因为 ,所以
,所以 ,于是点
,于是点 在
在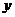 轴上.
轴上.因为
 ,所以
,所以 ,
, .
.设
 (
( ),由
),由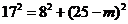 ,解得
,解得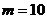 ,
,所以
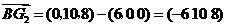 .
.设
 和平面
和平面 所成的角是
所成的角是 ,则
,则 .
.故直线
 与平面
与平面 所成的角是
所成的角是 .
. -
35.
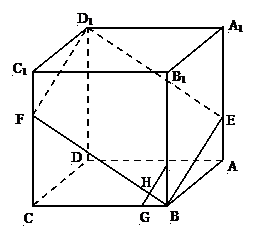 (江苏•理•18题)如图,已知
(江苏•理•18题)如图,已知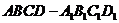 是棱长为3的正方体,点
是棱长为3的正方体,点 在
在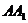 上,点
上,点 在
在 上,且
上,且 。
。(I)求证:
 四点共面;(4分)
四点共面;(4分)(II)若点
 在
在 上,
上, ,点
,点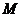 在
在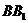 上,
上, ,垂足为
,垂足为 ,求证:
,求证: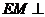 面
面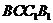 ;
; (Ⅲ)用
(Ⅲ)用 表示截面
表示截面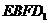 和面
和面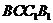 所成锐二面角大小,求
所成锐二面角大小,求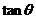 。
。 -
36.(江西•理•20题)右图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3。
(I)设点O是AB的中点,证明:OC∥平面A1B1C1;
(II)求二面角B-AC-A1的大小;
(Ⅲ)求此几何体的体积;
解法一:
(1)证明:作
 交
交 于
于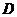 ,连
,连 .
.则
 .
.因为
 是
是 的中点,
的中点, 所以
所以 .
.则
 是平行四边形,因此有
是平行四边形,因此有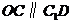 .
. 平面
平面 且
且 平面
平面 ,
,则
 面
面 .
.(2)如图,过
 作截面
作截面 面
面 ,分别交
,分别交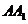 ,
, 于
于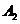 ,
, .
.作
 于
于 ,连
,连 .
.因为
 面
面 ,所以
,所以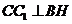 ,则
,则 平面
平面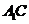 .
.又因为
 ,
,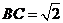 ,
, .
.所以
 ,根据三垂线定理知
,根据三垂线定理知 ,所以
,所以 就是所求二面角的平面角.
就是所求二面角的平面角.因为
 ,所以
,所以 ,故
,故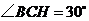 ,
,即:所求二面角的大小为
 .
.(3)因为
 ,所以
,所以 .
. .
.所求几何体体积为
 .
.解法二:
(1)如图,以
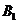 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,则
 ,
, ,
,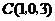 ,因为
,因为 是
是 的中点,所以
的中点,所以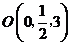 ,
,
 .
.易知,
 是平面
是平面 的一个法向量.
的一个法向量.因为
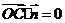 ,
, 平面
平面 ,所以
,所以 平面
平面 .
.(2)
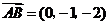 ,
,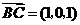 ,
,设
 是平面
是平面 的一个法向量,则
的一个法向量,则则
 ,
, 得:
得: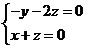
取
 ,
, .
.显然,
 为平面
为平面 的一个法向量.
的一个法向量.则
 ,结合图形可知所求二面角为锐角.
,结合图形可知所求二面角为锐角.所以二面角
 的大小是
的大小是 .
.(3)同解法一.
-
37.(辽宁•理•18题)如图,在直三棱柱
 中,
中, ,
, ,
, 分别为棱
分别为棱 的中点,
的中点,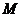 为棱
为棱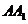 上的点,二面角
上的点,二面角 为
为 。
。(I)证明:
 ;
;
 (II)求
(II)求 的长,并求点
的长,并求点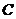 到平面
到平面 的距离。
的距离。 -
38.(宁夏•理•19题)如图,在三棱锥
 中,侧面
中,侧面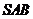 与侧面
与侧面 均为等边三角形,
均为等边三角形, ,
, 为
为 中点.
中点.(Ⅰ)证明:
 平面
平面 ;(Ⅱ)求二面角
;(Ⅱ)求二面角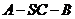 的余弦值.
的余弦值.证明:
(Ⅰ)由题设
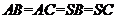
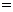
 ,连结
,连结 ,
,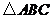 为等腰直角三角形,所以
为等腰直角三角形,所以 ,且
,且 ,又
,又 为等腰三角形,故
为等腰三角形,故 ,且
,且 ,从而
,从而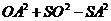 .
.所以
 为直角三角形,
为直角三角形, .
.又
 .
.所以
 平面
平面 .
.(Ⅱ)解法一:
取
 中点
中点 ,连结
,连结 ,由(Ⅰ)知
,由(Ⅰ)知 ,得
,得 .
. 为二面角
为二面角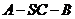 的平面角.
的平面角.由
 得
得 平面
平面 .
.所以
 ,又
,又 ,故
,故 .
. 所以二面角
所以二面角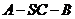 的余弦值为
的余弦值为 .
.解法二:
以
 为坐标原点,射线
为坐标原点,射线 分别为
分别为 轴、
轴、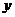 轴的正半轴,建立如图的空间直角坐标系
轴的正半轴,建立如图的空间直角坐标系 .
.设
 ,则
,则 .
. 的中点
的中点 ,
,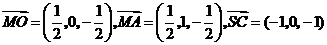 .
. .
.故
 等于二面角
等于二面角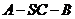 的平面角.
的平面角. ,
,所以二面角
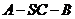 的余弦值为
的余弦值为 .
. -
39.(陕西•理•19题)如图,在底面为直角梯形的四棱锥
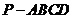 中
中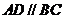 ,
,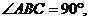

 ,
, ,BC=6。
,BC=6。(Ⅰ)求证:
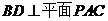 ;(Ⅱ)求二面角
;(Ⅱ)求二面角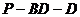 的大小;
的大小;解法一:(Ⅰ)
 平面
平面 ,
,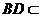 平面
平面 .
. .
.又
 ,
, .
. ,
,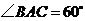 ,
, ,即
,即 .
.又
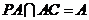 .
. 平面
平面 .
.(Ⅱ)过
 作
作 ,垂足为
,垂足为 ,连接
,连接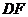 .
. 平面
平面 ,
, 是
是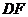 在平面
在平面 上的射影,由三垂线定理知
上的射影,由三垂线定理知 ,
, 为二面角
为二面角 的平面角.
的平面角. 又
又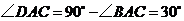 ,
,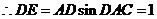 ,
, ,
,又
 ,
,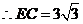 ,
, .
.由
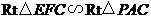 得
得 .
.在
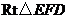 中,
中, ,
, .
. 二面角
二面角 的大小为
的大小为 .
.解法二:(Ⅰ)如图,建立坐标系,
则
 ,
, ,
, ,
,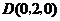 ,
, ,
, ,
, ,
, ,
,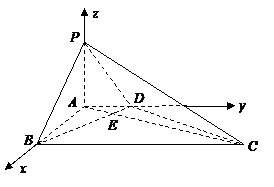
 ,
,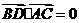 .
. ,
, ,
,又
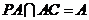 ,
, 平面
平面 .
.(Ⅱ)设平面
 的法向量为
的法向量为 ,
,则
 ,
, ,
,又
 ,
, ,
, 解得
解得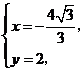

平面
 的法向量取为
的法向量取为 ,
, ,
, .
. 二面角
二面角 的大小为
的大小为 .
. -
40.
 (上海•理•19题)体积为1的直三棱柱
(上海•理•19题)体积为1的直三棱柱 中,
中, ,
, ,求直线
,求直线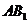 与平面
与平面 所成角。
所成角。
-
41.(四川•理•19题)如图,四边形
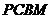 是直角梯形,∠
是直角梯形,∠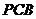 =90°,
=90°,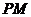 ∥
∥ ,
,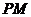 =1,
=1, =2,又
=2,又 =1,∠
=1,∠ =120°,
=120°, ⊥
⊥ ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°.(Ⅰ)求证:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求二面角
 的大小;
的大小;(Ⅲ)求三棱锥
 的体积;
的体积;分析:本题主要考察异面直线所成的角、平面与平面垂直、二面角、三棱锥体积等有关知识,考察思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力。
解法一:
(Ⅰ)∵
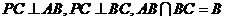
∴
 ,
,又∵

∴

(Ⅱ)取
 的中点
的中点 ,则
,则 ,连结
,连结 ,
,∵
 ,∴
,∴ ,从而
,从而
作
 ,交
,交 的延长线于
的延长线于 ,连结
,连结 ,则由三垂线定理知,
,则由三垂线定理知, ,
,从而
 为二面角
为二面角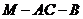 的平面角
的平面角直线
 与直线
与直线 所成的角为
所成的角为
∴

在
 中,由余弦定理得
中,由余弦定理得
在
 中,
中,
在
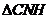 中,
中,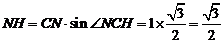
在
 中,
中,
故二面角
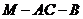 的平面角大小为
的平面角大小为
(Ⅲ)由(Ⅱ)知,
 为正方形
为正方形∴

解法二:(Ⅰ)同解法一
 (Ⅱ)在平面
(Ⅱ)在平面 内,过
内,过 作
作 ,建立空间直角坐标系
,建立空间直角坐标系 (如图)
(如图)由题意有
 ,设
,设 ,
,则

由直线
 与直线
与直线 所成的解为
所成的解为 ,得
,得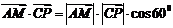 ,即
,即 ,解得
,解得
∴
 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,
,则
 ,取
,取 ,得
,得
平面
 的法向量取为
的法向量取为
设
 与
与 所成的角为
所成的角为 ,则
,则
显然,二面角
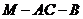 的平面角为锐角,
的平面角为锐角,故二面角
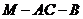 的平面角大小为
的平面角大小为
(Ⅲ)取平面
 的法向量取为
的法向量取为 ,则点A到平面
,则点A到平面 的距离
的距离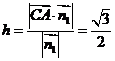
∵
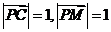 ,∴
,∴
-
42.
 (天津•理•19题)如图,在四棱锥
(天津•理•19题)如图,在四棱锥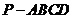 中,
中, 底面
底面 ,
, ,
, ,
, 是
是 的中点.
的中点.(Ⅰ)证明
 ;
;(Ⅱ)证明
 平面
平面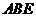 ;
;(Ⅲ)求二面角
 的大小;
的大小;分析:本小题考查直线与直线垂直、直线与平面垂直、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.满分12分.
解答:(Ⅰ)证明:在四棱锥
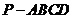 中,因
中,因 底面
底面 ,
, 平面
平面 ,故
,故 .
. ,
,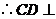 平面
平面 .
.而
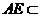 平面
平面 ,
, .
.(Ⅱ)证明:由
 ,
,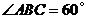 ,可得
,可得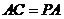 .
.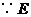 是
是 的中点,
的中点,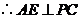 .
.由(Ⅰ)知,
 ,且
,且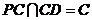 ,所以
,所以 平面
平面 .
.而
 平面
平面 ,
,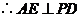 .
.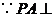 底面
底面 在底面
在底面 内的射影是
内的射影是 ,
, ,
, .
.又
 ,综上得
,综上得 平面
平面 .
. (Ⅲ)解法一:过点
(Ⅲ)解法一:过点 作
作 ,垂足为
,垂足为 ,连结
,连结 .则(Ⅱ)知,
.则(Ⅱ)知, 平面
平面 ,
, 在平面
在平面 内的射影是
内的射影是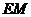 ,则
,则 .
.因此
 是二面角
是二面角 的平面角.
的平面角.由已知,得
 .设
.设 ,
,可得
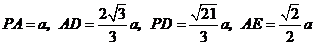 .
.在
 中,
中,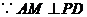 ,
, ,
,则
 .在
.在 中,
中,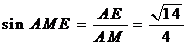 .
.所以二面角
 的大小是
的大小是 .
.解法二:由题设
 底面
底面 ,
,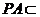 平面
平面 ,则平面
,则平面 平面
平面 ,交线为
,交线为 .
.过点
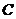 作
作 ,垂足为
,垂足为 ,故
,故 平面
平面 .过点
.过点 作
作 ,垂足为
,垂足为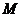 ,连结
,连结 ,故
,故 .因此
.因此 是二面角
是二面角 的平面角.
的平面角.由已知,可得
 ,设
,设 ,
,可得
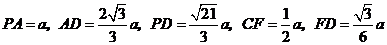 .
.
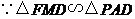 ,
, .
.于是,
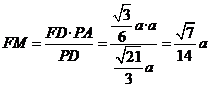 .
.在
 中,
中,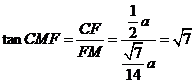 .
.所以二面角
 的大小是
的大小是 .
. -
43.
 (浙江•理•19题)在如图所示的几何体中,
(浙江•理•19题)在如图所示的几何体中, 平面ABC,
平面ABC, 平面ABC,
平面ABC,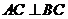 ,
, ,M是AB的中点。
,M是AB的中点。(Ⅰ)求证:
 ;
;(Ⅱ)求CM与平面CDE所成的角;
分析:本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.满分14分.
解答:
方法一:
(I)证明:因为
 ,
, 是
是 的中点,
的中点,所以
 .
.又
 平面
平面 ,
,所以
 .
.(II)解:过点
 作
作 平面
平面 ,垂足是
,垂足是 ,连结
,连结 交延长交
交延长交 于点
于点 ,连结
,连结 ,
, .
.
 是直线
是直线 和平面
和平面 所成的角.
所成的角.因为
 平面
平面 ,
,所以
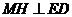 ,
,又因为
 平面
平面 ,
,所以
 ,
,则
 平面
平面 ,因此
,因此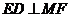 .
.设
 ,
, ,
,在直角梯形
 中,
中, ,
,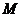 是
是 的中点,
的中点,所以
 ,
, ,
, ,
,得
 是直角三角形,其中
是直角三角形,其中 ,
,所以
 .
.在
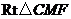 中,
中, ,
,所以
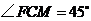 ,
,故
 与平面
与平面 所成的角是
所成的角是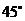 .
.方法二:
如图,以点
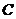 为坐标原点,以
为坐标原点,以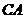 ,
, 分别为
分别为 轴和
轴和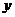 轴,过点
轴,过点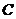 作与平面
作与平面 垂直的直线为
垂直的直线为 轴,建立直角坐标系
轴,建立直角坐标系 ,设
,设 ,则
,则 ,
, ,
, .
. ,
, .
.(I)证明:因为
 ,
, ,
,所以
 ,
,故
 .
.(II)解:设向量
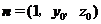 与平面
与平面 垂直,则
垂直,则 ,
, ,
, 即
即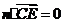 ,
, .
.因为
 ,
,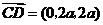 ,
,所以
 ,
, ,
,即
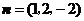 ,
, ,
,直线
 与平面
与平面 所成的角
所成的角 是
是 与
与 夹角的余角,
夹角的余角,所以
 ,
,因此直线
 与平面
与平面 所成的角是
所成的角是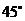 .
.