-
网址:http://m.1010jiajiao.com/paper/timu/5157707.html[举报]
31.(福建•理•18题)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。
(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)求点C到平面A1BD的距离;
分析:本小题主要考查直线与平面的位置关系,二面角的大小,点到平面的距离等知识,考查空间想象能力、逻辑思维能力和运算能力.满分12分.
解答:解法一:(Ⅰ)取
 中点
中点 ,连结
,连结 .
. 为正三角形,
为正三角形, .
.
 正三棱柱
正三棱柱 中,平面
中,平面 平面
平面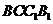 ,
,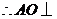 平面
平面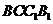 .
.连结
 ,在正方形
,在正方形 中,
中, 分别为
分别为 的中点,
的中点, ,
, .
.在正方形
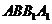 中,
中, ,
,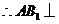 平面
平面 .
.(Ⅱ)设
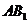 与
与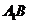 交于点
交于点 ,在平面
,在平面 中,作
中,作 于
于 ,连结
,连结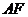 ,由(Ⅰ)得
,由(Ⅰ)得 平面
平面 .
. ,
,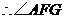 为二面角
为二面角 的平面角.
的平面角.在
 中,由等面积法可求得
中,由等面积法可求得 ,
,又
 ,
,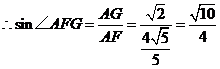 .
.所以二面角
 的大小为
的大小为 .
.(Ⅲ)
 中,
中, ,
, .
.在正三棱柱中,
 到平面
到平面 的距离为
的距离为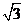 .
.设点
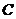 到平面
到平面 的距离为
的距离为 .
.由
 得
得 ,
,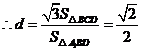 .
. 点
点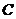 到平面
到平面 的距离为
的距离为 .
.解法二:(Ⅰ)取
 中点
中点 ,连结
,连结 .
. 为正三角形,
为正三角形, .
. 在正三棱柱
在正三棱柱 中,平面
中,平面 平面
平面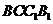 ,
, 平面
平面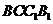 .
.取
 中点
中点 ,以
,以 为原点,
为原点,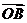 ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
,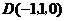 ,
, ,
, ,
,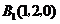 ,
, ,
, ,
, .
. ,
, ,
,
 ,
, .
.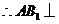 平面
平面 .
.(Ⅱ)设平面
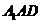 的法向量为
的法向量为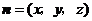 .
.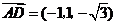 ,
, .
.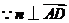 ,
, ,
,

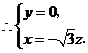
令
 得
得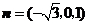 为平面
为平面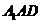 的一个法向量.
的一个法向量.由(Ⅰ)知
 平面
平面 ,
, 为平面
为平面 的法向量.
的法向量. ,
,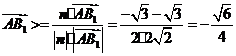 .
. 二面角
二面角 的大小为
的大小为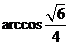 .
.(Ⅲ)由(Ⅱ),
 为平面
为平面 法向量,
法向量, .
. 点
点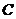 到平面
到平面 的距离
的距离 .
. - 题目来源:高考数学立体几何试题汇编