题目内容

18．某走时准确的时钟，分针与时针的长度之比是1.2：1．
（1）分针与时针的角速度之比是多少？
（2）分针针尖与时针针尖的线速度之比是多少？
（3）分针和时针的运动可看做匀速圆周运动，则分针和时针转动的向心加速度之比是多少？

分析 （1）时针和分针都是做匀速圆周运动，根据转过的角度之间的关系可以求得角速度之比；
（2）由V=rω可求得线速度之比；
（3）根据a=vω求出向心加速度大小之比．

解答 解：（1）在一个小时的时间内，分针每转过的角度为360度，而时针转过的角度为30度，
所以角速度之比为：ω1：ω2=360：30=12：1，
（2）由V=rω可得，线速度之比为v1：v2=1.2×12：1×1=14.4：1；
（3）根据a=vω知，向心加速度之比为a1：a2=172.8：1
答：（1）分针与时针的角速度之比是12：1；
（2）分针针尖与时针针尖的线速度之比是14.4：1；
（3）分针和时针转动的向心加速度之比是172.8：1．

点评 本题关键是建立圆周运动的运动模型，然后结合线速度、角速度、周期、转速间的关系列式分析，基础题目．

练习册系列答案
相关题目
8．如图所示，有一矩形线圈在竖直平面上从静止开始下落，当线圈的下边垂直磁感线方向进入匀强磁场，而上边还未进入匀强磁场的过程中，线圈不可能做的运动是（　　）
A．匀速下落B．加速下落C．减速下落D．匀减速下落
9．关于单摆的运动有下列说法，正确的是（　　）
①单摆的回复力是重力沿摆球运动轨迹切向的分力
②单摆的回复力是摆线的拉力与重力的合力
③单摆的周期与质量无关与振幅无关，与摆长和当地的重力加速度有关
④单摆做简谐运动的条件是摆角很小如小于5°
⑤在山脚下走时准确的摆钟移到高山上走时将变快．
A．①③④B．②③④C．③④⑤D．①④⑤
6．A、B两个质点分别做匀速圆周运动，在相同的时间内它们通过的路程之比sA：sB=4：3，转过的角度之比θA：θB=3：2，则他们的向心加速度之比是（　　）
A．4：3B．3：2C．2：1D．1：2
13．在某介质中形成一列简谐横波，该横波上有相距4m的A、B两点，质点B靠近波源，如图所示为A、B两质点的振动图象，若这列波的波长大于2m，则这列波的波速可能为（　　）
A．40m/sB．8m/sC．$\frac{40}{3}$m/sD．$\frac{40}{7}$m/s
3．滑板运动是一项非常刺激的水上运动．研究表明，在进行滑板运动时，水对滑板的作用力FN垂直于板面，大小为kv2，其中v为滑板速率（水可视为静止）．某次运动中，在水平牵引力作用下，当滑板和水面的夹角θ=37°时（如图），滑板做匀速直线运动，相应的k=54kg/m，人和滑板的总质量为108kg，试求（重力加速度g取10m/s2，sin37°取$\frac{3}{5}$，忽略空气阻力）：
（1）水平牵引力的大小；
（2）滑板的速率．
10．如图所示，在边长为a的正方形区域内有以对角线为边界，垂直于纸面的两个方向相反的匀强磁场，两磁场的磁感应强度大小相等．纸面内一边长为a的正方形导线框沿着x轴匀速穿过磁场区域，在t=0时，导线框运动到原点O处且恰好开始进入磁场区域．取顺时针方向为导线框中感应电流的正方向，则下列图象中能够正确表示从t=0时刻开始感应电流与导线框位移关系的是（　　）
A．B．C．D．
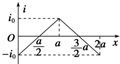
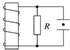7．两块水平放置的金属板间距离为d，用导线与一个n匝线圈相连，线圈电阻为r，线圈中有竖直方向的磁场，电阻R与金属板连接，如图所示，两板间有一个质量为m、电荷量+q的油滴恰好处于静止，则线圈中的磁通量的变化率是$\frac{mgd（R+r）}{nqR}$．
8．如图所示，用平行于斜面的力F把质量为m的物体沿粗糙斜面上拉，斜面与水平面的夹角θ=30°，物体与斜面的动摩擦因数μ=$\frac{\sqrt{3}}{6}$，并使其加速度大小等于该物体放在斜面上沿斜面下滑时的加速度大小，则F的大小是（　　）
A．$\frac{1}{4}$mgB．$\frac{1}{2}$mgC．mgD．$\frac{3}{4}$mg

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网