题目内容
7.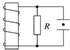 两块水平放置的金属板间距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量+q的油滴恰好处于静止,则线圈中的磁通量的变化率是$\frac{mgd(R+r)}{nqR}$.
两块水平放置的金属板间距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量+q的油滴恰好处于静止,则线圈中的磁通量的变化率是$\frac{mgd(R+r)}{nqR}$.
分析 电荷量+q的油滴恰好静止金属板间,受到的电场力与重力平衡,线圈的上端是电源的负极.由于线圈中有竖直向上均匀变化的磁场,根据楞次定律,磁场应是均匀增加的.
解答 解:由于带正电的油滴恰好处于静止状态,所以上极板带负电,线圈的上端是电源的负极.
由于线圈中有竖直向上均匀变化的磁场,根据楞次定律,磁场应是均匀增加的.
根据带电油滴的平衡,有:
mg=q$\frac{U}{d}$
解得:
U=$\frac{mgd}{q}$ 其中U为两板间的电势差.
由闭合电路的欧姆定律和串联电路的知识可知:
U=$\frac{R}{R+r}$E=$\frac{R}{R+r}$n$\frac{△Φ}{△t}$
则$\frac{△Φ}{△t}$=$\frac{mgd(R+r)}{nqR}$
故答案为:$\frac{mgd(R+r)}{nqR}$.
点评 本题是电磁感应与电路、电场、力学等知识的简单综合;对于电磁感应问题,要楞次定律判断感应电动势、法拉第定律研究感应电动势大小是常用的思路.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
17. 某同学在做“用单摆测重力加速度”的实验时,测量5种不同摆长情况下单摆的振动周期,记录数据如下:
某同学在做“用单摆测重力加速度”的实验时,测量5种不同摆长情况下单摆的振动周期,记录数据如下:
(1)以摆长L为横坐标,周期的平方T2为纵坐标,根据以上数据在图中画出T2-L的图线.
(2)由此图象求出重力加速度g=9.86m/s2.(结果保留到小数点后二位)
 某同学在做“用单摆测重力加速度”的实验时,测量5种不同摆长情况下单摆的振动周期,记录数据如下:
某同学在做“用单摆测重力加速度”的实验时,测量5种不同摆长情况下单摆的振动周期,记录数据如下:| 摆长L/m | 0.50 | 0.80 | 0.90 | 1.00 | 1.20 |
| 周期T/s | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
(2)由此图象求出重力加速度g=9.86m/s2.(结果保留到小数点后二位)
2. 如图所示,有一个质量为M,半径为R,密度均匀的大球体.从中挖去一个半径为$\frac{R}{2}$的小球体,并在空腔中心放置一质量为m的质点,则大球体的剩余部分对该质点的万有引力大小为(已知质量分布均匀的球壳对壳内物体的引力为零)( )
如图所示,有一个质量为M,半径为R,密度均匀的大球体.从中挖去一个半径为$\frac{R}{2}$的小球体,并在空腔中心放置一质量为m的质点,则大球体的剩余部分对该质点的万有引力大小为(已知质量分布均匀的球壳对壳内物体的引力为零)( )
 如图所示,有一个质量为M,半径为R,密度均匀的大球体.从中挖去一个半径为$\frac{R}{2}$的小球体,并在空腔中心放置一质量为m的质点,则大球体的剩余部分对该质点的万有引力大小为(已知质量分布均匀的球壳对壳内物体的引力为零)( )
如图所示,有一个质量为M,半径为R,密度均匀的大球体.从中挖去一个半径为$\frac{R}{2}$的小球体,并在空腔中心放置一质量为m的质点,则大球体的剩余部分对该质点的万有引力大小为(已知质量分布均匀的球壳对壳内物体的引力为零)( )| A. | G$\frac{Mm}{R^2}$ | B. | 0 | C. | 4G$\frac{Mm}{R^2}$ | D. | G$\frac{Mm}{{2{R^2}}}$ |
19.关于做平抛运动物体的速度和加速度,下列说法正确的是( )
| A. | 速度的大小不变,方向不断变化 | B. | 加速度大小和方向都在不断变化 | ||
| C. | 加速度的大小和方向都不变 | D. | 加速度的大小不变,方向不断变化 |
2. 如图所示,半径为R的半圆形光滑凹槽A静止在光滑平面上,其质量为m,现有一质量也为m的小物块B,由静止开始从槽面左端的最高点沿凹槽滑下,当小物块B刚要到达槽面最低点时,凹槽A恰好被一表面带有粘性物质的固定挡板粘住,在极短的时间内速度减为零;小物块B继续向右运动,运动到距槽面最低点的最大高度是$\frac{R}{2}$,则小物块从释放到第一次到达最低点的过程中,下列说法正确的是( )
如图所示,半径为R的半圆形光滑凹槽A静止在光滑平面上,其质量为m,现有一质量也为m的小物块B,由静止开始从槽面左端的最高点沿凹槽滑下,当小物块B刚要到达槽面最低点时,凹槽A恰好被一表面带有粘性物质的固定挡板粘住,在极短的时间内速度减为零;小物块B继续向右运动,运动到距槽面最低点的最大高度是$\frac{R}{2}$,则小物块从释放到第一次到达最低点的过程中,下列说法正确的是( )
 如图所示,半径为R的半圆形光滑凹槽A静止在光滑平面上,其质量为m,现有一质量也为m的小物块B,由静止开始从槽面左端的最高点沿凹槽滑下,当小物块B刚要到达槽面最低点时,凹槽A恰好被一表面带有粘性物质的固定挡板粘住,在极短的时间内速度减为零;小物块B继续向右运动,运动到距槽面最低点的最大高度是$\frac{R}{2}$,则小物块从释放到第一次到达最低点的过程中,下列说法正确的是( )
如图所示,半径为R的半圆形光滑凹槽A静止在光滑平面上,其质量为m,现有一质量也为m的小物块B,由静止开始从槽面左端的最高点沿凹槽滑下,当小物块B刚要到达槽面最低点时,凹槽A恰好被一表面带有粘性物质的固定挡板粘住,在极短的时间内速度减为零;小物块B继续向右运动,运动到距槽面最低点的最大高度是$\frac{R}{2}$,则小物块从释放到第一次到达最低点的过程中,下列说法正确的是( )| A. | 凹槽A对小物块B做的功W=-$\frac{1}{2}$mgR | |
| B. | 凹槽A对小物块B做的功W=mgR | |
| C. | 凹槽A被粘住的瞬间,小物块B对凹槽A的压力大小为mg | |
| D. | 凹槽A被粘住的瞬间,小物块B对凹槽A的压力大小为2mg |
 如图为一小球做平抛运动的闪光照片的一部分.图中方格每边长为5cm,g取10m/s2.求小球的水平分速度2m/s,小球在B点时的竖直分速度3m/s.
如图为一小球做平抛运动的闪光照片的一部分.图中方格每边长为5cm,g取10m/s2.求小球的水平分速度2m/s,小球在B点时的竖直分速度3m/s. 如图所示,细绳一端系着一个质量为M=0.5kg的物体A,另一端通过光滑的小孔吊着质量为m=0.3kg的物体B,M的中点与圆孔的距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,若物体A相对水平面静止,物体B始终处于静止状态,平面转动的角速度ω最小值为$\sqrt{10}$rad/s,最大值为$5\sqrt{2}$rad/s (g=10m/s2)
如图所示,细绳一端系着一个质量为M=0.5kg的物体A,另一端通过光滑的小孔吊着质量为m=0.3kg的物体B,M的中点与圆孔的距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,若物体A相对水平面静止,物体B始终处于静止状态,平面转动的角速度ω最小值为$\sqrt{10}$rad/s,最大值为$5\sqrt{2}$rad/s (g=10m/s2)