题目内容
3.游泳运动员要渡过一条宽d=100m的河,已知运动员在静水中的速度为V1=5m/s,水流速度为V2=3m/s,求:运动员以最短距离过河时,他用了多长的时间( )| A. | 20s | B. | 25s | C. | 50s | D. | $\frac{200}{3}$s |
分析 由矢量合成的平行四边形定则得知小船的合速度,小船实际以合速度做匀速直线运动,进而求得位移的大小;小船以最短距离过河时,则静水中的速度斜着向上游,合速度垂直河岸.
解答 解:小船以最短距离过河时,则静水中的速度斜着向上游,合速度垂直河岸,设与河岸的夹角为θ,
则由矢量合成的平行四边形法则解三角形得:cosθ=$\frac{{v}_{2}}{{v}_{1}}$=$\frac{3}{5}$,
这时船头与河水速度夹角为θ=37°
那么船垂直河岸行驶的速度为v=$\sqrt{{5}^{2}-{3}^{2}}$m/s=4m/s;
所以渡河时间t=$\frac{100}{4}$s=25s;
故选:B.
点评 小船过河问题属于运动的合成问题,要明确分运动的等时性、独立性,运用分解的思想,看过河时间只分析垂直河岸的速度,分析过河位移时,要分析合速度.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
13.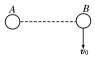 如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
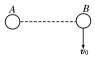 如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )| A. | 若A、B为异种电荷,B球可能做圆周运动 | |
| B. | 若A、B为异种电荷,B球一定做加速度、速度均变小的曲线运动 | |
| C. | 若A、B为同种电荷,B球一定做远离A的变加速曲线运动 | |
| D. | 若A、B为同种电荷,B球的动能一定会减小 |
14.一物体以初速度v0=20m/s沿光滑斜面匀减速向上滑动,当上滑距离x0=30m时,速度减为10m/s,物体恰滑到斜面顶部停下,则斜面长度为( )
| A. | 40 m | B. | 50 m | C. | 32 m | D. | 60 m |
18. 如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )
如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )
 如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )
如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )| A. | 物体的实际运动速度为v1+v2 | B. | 物体相对地面做曲线运动 | ||
| C. | 绳索始终保持竖直状态 | D. | 物体实际运动方向始终竖直向上 |
7.在探究“弹力和弹簧伸长的关系”时,小明同学用如图甲所示的实验装置进行实验;将该弹簧竖直悬挂起来,在自由端挂上砝码盘.通过改变盘中砝码的质量,测得实验数据如下:
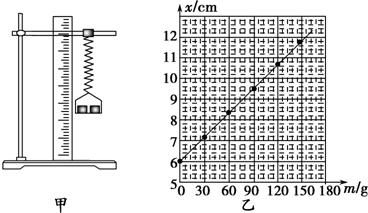
(1)小明同学根据实验数据在坐标纸上用描点法画出x-m图象如图乙所示,根据图象他得出结论:弹簧弹力和弹簧伸长量不是正比例关系,而是一次函数关系,他的结论错误的原因是:x-m图象纵坐标不是弹簧的伸长量.
(2)作出的图线与坐标系纵轴有一截距,其物理意义是未挂钩码时弹簧的长度;该弹簧的劲度系数k=25.0N/m(结果保留3位有效数字).
(3)请你判断该同学得到的劲度系数与考虑砝码盘的质量相比,结果相同(填“偏大”、“偏小”或“相同”).

| 1 | 2 | 3 | 4 | 5 | 6 | |
| 钩码质量m/g | 0 | 30 | 60 | 90 | 120 | 150 |
| 刻度尺读数/cm | 6.00 | 7.14 | 8.34 | 9.48 | 10.64 | 11.79 |
(2)作出的图线与坐标系纵轴有一截距,其物理意义是未挂钩码时弹簧的长度;该弹簧的劲度系数k=25.0N/m(结果保留3位有效数字).
(3)请你判断该同学得到的劲度系数与考虑砝码盘的质量相比,结果相同(填“偏大”、“偏小”或“相同”).
5.一电子飞经电场中A、B两点,电子在A点的电势能4.8×10-17J,动能为3.2×10-17J,电子经过B点的电势能为3.2×10-17J,如果电子只受电场力作用,则( )
| A. | 电子在B点的动能为4.8×10-17J | B. | 由A点到B点电场力做功为100eV | ||
| C. | 电子在B点的动能为1.6×10-17J | D. | A、B两点间电势差为100V |
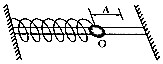 一质点作简谐振动,它离开平衡的位移s(厘米)与时间t(秒)的关系为s=10sin(6πt+$\frac{π}{6}$).
一质点作简谐振动,它离开平衡的位移s(厘米)与时间t(秒)的关系为s=10sin(6πt+$\frac{π}{6}$).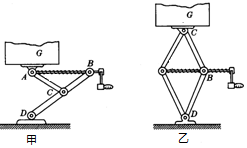 如图所示是汽年内常备的两种类型的“千斤顶”,是用于汽车换轮胎的顶升机,甲是“Y形”的,乙是“菱形”的,顺时钟摇动手柄,使螺旋杆转动,A,B间距离变小,重物G就被顶升起来,反之则可使G下降,若顶升的是汽车本身,便能进行换轮胎的操作了,若物重为G,AB与AC间的夹角为θ,此时螺杆AB的拉力为多少?
如图所示是汽年内常备的两种类型的“千斤顶”,是用于汽车换轮胎的顶升机,甲是“Y形”的,乙是“菱形”的,顺时钟摇动手柄,使螺旋杆转动,A,B间距离变小,重物G就被顶升起来,反之则可使G下降,若顶升的是汽车本身,便能进行换轮胎的操作了,若物重为G,AB与AC间的夹角为θ,此时螺杆AB的拉力为多少?