题目内容
5.一电子飞经电场中A、B两点,电子在A点的电势能4.8×10-17J,动能为3.2×10-17J,电子经过B点的电势能为3.2×10-17J,如果电子只受电场力作用,则( )| A. | 电子在B点的动能为4.8×10-17J | B. | 由A点到B点电场力做功为100eV | ||
| C. | 电子在B点的动能为1.6×10-17J | D. | A、B两点间电势差为100V |
分析 根据能量守恒求出电子的动能,根据电场力做功与电势能的变化关系求电场力做的功,同时可以求出两点间的电势差.
解答 解:AC、因只有电场力做功,故电子的电势能和动能总和保持不变;在A点,总能量为:E=EKA+EPA=3.2×10-17+4.8×10-17=8×10-17J,则根据能量守恒定律可知,在B点动能 EKB=E-EPB=8×10-17-3.2×10-17=4.8×10-17J,故A正确,C错误;
B、电场力做的功等于电势能的减少量,所以由A点到B点电场力做功为 WAB=EPA-EPB=4.8×10-17J-3.2×10-17J=1.6×10-17J=100ev,故B正确;
D、由WAB=-eUAB,所以UAB=$\frac{{W}_{AB}}{-e}$=$\frac{-100eV}{-e}$-100V,故D正确;
故选:ABD
点评 本题的关键要掌握电场力做功与电势能的变化关系WAB=EPA-EPB这个关系式,结合能量守恒即可解决此类题目.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
3.游泳运动员要渡过一条宽d=100m的河,已知运动员在静水中的速度为V1=5m/s,水流速度为V2=3m/s,求:运动员以最短距离过河时,他用了多长的时间( )
| A. | 20s | B. | 25s | C. | 50s | D. | $\frac{200}{3}$s |
10.如图(甲)所示,面积S=0.2m2的线圈,匝数n=630匝,总电阻r=1.0Ω,线圈处在变化的磁场中,设磁场垂直纸面向外为正方向,磁感应强度B随时间t按图(乙)所示规律变化,方向垂直线圈平面,图(甲)中传感器可看成一个纯电阻R,并标有“3V,0.9W”,滑动变阻器R0上标有“10Ω,1A”,则下列说法正确的是( )
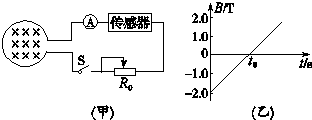

| A. | 电流表的电流方向向左 | |
| B. | 为了保证电路的安全,电路中允许通过的最大电流为1 A | |
| C. | 线圈中产生的感应电动势随时间在变化 | |
| D. | 若滑动变阻器的滑片置于最左端,为了保证电路的安全,图(乙)中的t0最小值为40 s |
17.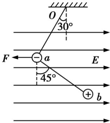 两带等量异种电荷的小球用轻质细线悬挂于O点并置于水平向右的匀强电场E中,如图所示,a处小球带负电、质量为2mg,b处小球带正电、质量为mg,今用水平力F拉a处小球,整个装置处于平衡状态时,细线Oa与竖直方向的夹角为30°,细线ab与竖直方向的夹角为45°,则力F的大小为( )
两带等量异种电荷的小球用轻质细线悬挂于O点并置于水平向右的匀强电场E中,如图所示,a处小球带负电、质量为2mg,b处小球带正电、质量为mg,今用水平力F拉a处小球,整个装置处于平衡状态时,细线Oa与竖直方向的夹角为30°,细线ab与竖直方向的夹角为45°,则力F的大小为( )
 两带等量异种电荷的小球用轻质细线悬挂于O点并置于水平向右的匀强电场E中,如图所示,a处小球带负电、质量为2mg,b处小球带正电、质量为mg,今用水平力F拉a处小球,整个装置处于平衡状态时,细线Oa与竖直方向的夹角为30°,细线ab与竖直方向的夹角为45°,则力F的大小为( )
两带等量异种电荷的小球用轻质细线悬挂于O点并置于水平向右的匀强电场E中,如图所示,a处小球带负电、质量为2mg,b处小球带正电、质量为mg,今用水平力F拉a处小球,整个装置处于平衡状态时,细线Oa与竖直方向的夹角为30°,细线ab与竖直方向的夹角为45°,则力F的大小为( )| A. | $\frac{2}{3}$mg | B. | mg | C. | $\frac{2\sqrt{3}}{3}$mg | D. | $\sqrt{3}$mg |
15.一个物体做匀变速直线运动,若运动的时间之比为t1:t2:t3:…=1:2:3:…以下说法正确的是( )
| A. | 相应的运动距离之比一定是S1:S2:S3:…=1:4:9:… | |
| B. | 相邻的相同时间内的位移之比一定是S1:S2:S3:…=1:3:5:… | |
| C. | 相邻的相同时间内位移之差值一定是△S=aT2,其中T为相同的时间间隔 | |
| D. | t1、t2、t3秒末的速度之比一定是v1:v2:v3:…=1:2:3:… |
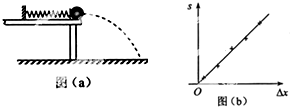 某同学利用下述装置对轻质弹簧的弹性势能进行探究,一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连:弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示.向左推小球,使弹簧压缩一段距离后由静止释放.小球离开桌面后落到水平地面.通过测量和计算,可求得弹簧被压缩后的弹性势能.回答下列问题:
某同学利用下述装置对轻质弹簧的弹性势能进行探究,一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连:弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示.向左推小球,使弹簧压缩一段距离后由静止释放.小球离开桌面后落到水平地面.通过测量和计算,可求得弹簧被压缩后的弹性势能.回答下列问题: 如图所示,垂直纸面向里的匀强磁场的宽度为h1,矩形线圈abcd的质量为m=0.016kg,电阻R=0.1Ω,ab边的长度为l=0.5m.bc边的长度为d=0.1m,矩形线圈cd边到磁场的上边界的距离为h2=5m,矩形线圈从该位置由静止开始自由下落,线圈cd边刚进入磁场时恰好做匀速运动,线圈在下落过程中始终保持竖直,不计空气阻力,g=10m/s2,求:
如图所示,垂直纸面向里的匀强磁场的宽度为h1,矩形线圈abcd的质量为m=0.016kg,电阻R=0.1Ω,ab边的长度为l=0.5m.bc边的长度为d=0.1m,矩形线圈cd边到磁场的上边界的距离为h2=5m,矩形线圈从该位置由静止开始自由下落,线圈cd边刚进入磁场时恰好做匀速运动,线圈在下落过程中始终保持竖直,不计空气阻力,g=10m/s2,求: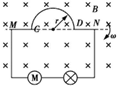 如图所示,半径为r=$\frac{1}{π}$m的半圆形单匝线圈$\widehat{CD}$在磁感应强度为B=$\sqrt{2}$T的磁场中绕轴线MN匀速转动给小型电动机和小灯泡(5V 10W)供电,线圈由电阻率为ρ=3×10-8Ω•m、横截面积S0=1×10-7m2的金属丝绕制而成,MC、DN两段的电阻不计,转速为n=10r/s,电动机线圈的电阻为R=0.4Ω,小灯泡恰能正常发光.
如图所示,半径为r=$\frac{1}{π}$m的半圆形单匝线圈$\widehat{CD}$在磁感应强度为B=$\sqrt{2}$T的磁场中绕轴线MN匀速转动给小型电动机和小灯泡(5V 10W)供电,线圈由电阻率为ρ=3×10-8Ω•m、横截面积S0=1×10-7m2的金属丝绕制而成,MC、DN两段的电阻不计,转速为n=10r/s,电动机线圈的电阻为R=0.4Ω,小灯泡恰能正常发光. 如图所示是某次实验中获得的小球下落时的频闪照片,频闪间隔是$\frac{1}{30}$s.根据此照片计算小球在4.90cm位置处的速度大小为0.984m/s;小球下落的加速度大小为9.77m/s2.(结果保留3位有效数字)
如图所示是某次实验中获得的小球下落时的频闪照片,频闪间隔是$\frac{1}{30}$s.根据此照片计算小球在4.90cm位置处的速度大小为0.984m/s;小球下落的加速度大小为9.77m/s2.(结果保留3位有效数字)