9.若直线2x+3y-1=0与直线4x+my+11=0平行,则它们之间的距离为( )
| A. | $\frac{{\sqrt{13}}}{2}$ | B. | $\frac{{2\sqrt{13}}}{13}$ | C. | $\frac{{6\sqrt{13}}}{13}$ | D. | $\frac{{12\sqrt{13}}}{13}$ |
8.设Sn=$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{n(n+1)}$,且Sn=$\frac{7}{8}$,则n的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
7.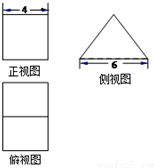 一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )
 一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )| A. | 64 | B. | 76 | C. | 88 | D. | 112 |
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=10,b=8,B=30°,那么△ABC的解的情况是( )
| A. | 无解 | B. | 一解 | C. | 两解 | D. | 一解或两解 |
4.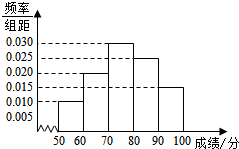 对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )
对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )
 对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )
对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )| A. | 0.09 | B. | 0.20 | C. | 0.25 | D. | 0.40 |
1.为调查某地区高三学生是否需要心理疏导,用简单随机抽样方法从该校调查了500位高三学生,结果如下:
(Ⅰ)估计该地区高三学生中,需要心理疏导的高三学生的百分比;
(Ⅱ)能否有99%的把握认为该地区高三学生是否需要心理疏导与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的抽样方法来调查估计该地区高三学生中,需要提供心理疏导的高三学生的比例?请说明理由.
附:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
0 247798 247806 247812 247816 247822 247824 247828 247834 247836 247842 247848 247852 247854 247858 247864 247866 247872 247876 247878 247882 247884 247888 247890 247892 247893 247894 247896 247897 247898 247900 247902 247906 247908 247912 247914 247918 247924 247926 247932 247936 247938 247942 247948 247954 247956 247962 247966 247968 247974 247978 247984 247992 266669
 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(Ⅱ)能否有99%的把握认为该地区高三学生是否需要心理疏导与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的抽样方法来调查估计该地区高三学生中,需要提供心理疏导的高三学生的比例?请说明理由.
附:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 10.828 |