题目内容

2．已知函数f（x）=[3x2+（2a-6）x+12-a]•ex有极大值和极小值，求实数a的取值范围．

分析 先求出函数的导数，根据函数有极大值和极小值得到关于导函数的方程有两个不同的实数根，由判别式大于0，解出a的范围即可．

解答 解：f′（x）=（3x2+2ax+a+6）•ex，
∵f（x）有极大值和极小值，
∴方程3x2+2ax+a+6=0有两个不同的实数解，
∴△=（2a）2-4（a+6）＞0，即a2-a-6＞0，
解得：a＜-2或a＞3．

点评 不同考查了函数的极值问题，考查导数的应用，二次方程的性质，是一道基础题．

练习册系列答案
相关题目
12．（2-x）10=a0+a1x+a2x2+…+a10x10．则a1+a2+a3+…+a10=（　　）
A．1B．-1C．1023D．-1023
13．在复平面内，O是坐标原点，向量$\overrightarrow{OA}$对应的复数是m2-8m+15+（m2+m-12）i．
（Ⅰ）当实数m取什么值时，点A在虚轴上；
（Ⅱ）当实数m取什么值时，点A位于第四象限．
10．已知函数f（x）=lnx，g（x）=x2-2af（x）（a∈R且a≠0）．
（1）若a=1，求函数g（x）在区间[1，2]上的最小值；
（2）若f（x）＜g（x）在x∈（1，+∞）上恒成立，求实数a的取值范围．
17．设（2x-1）5=a0+a1（x-1）+a2（x-1）2+…+a5（x-1）5，则a0+a1+a2+…+a5的值为（　　）
A．1B．-1C．243D．-243
7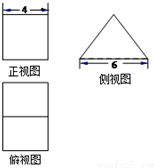．一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形，则该几何体的表面积是（　　）
A．64B．76C．88D．112
14．已知直线l：y=（1-m）x+m（m∈R）．
（Ⅰ）若直线l的倾斜角$α∈[\frac{π}{4}，\frac{π}{3}]$，求实数m的取值范围；
（Ⅱ）若直线l分别与x轴，y轴的正半轴交于A，B两点，O是坐标原点，求△AOB面积的最小值及此时直线l的方程．
11．在△ABC中，内角A，B，C所对边分别为a，b，c，且$\frac{c-b}{c-a}$=$\frac{sinA}{sinC+sinB}$．
（1）求角B的大小；
（2）如果b=2，求△ABC面积的最大值．
16．若不等式（m-2）x2+2（m-2）x-4＜0的解集为R，求实数m的范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网