题目内容
4．
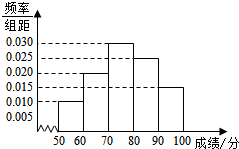对某次联考数学成绩（百分制）进行分析，如图为分析结果的频率分布直方图．根据标准，成绩分数在区间[50，60）上为不及格，在[60，70）上为一般，在[70，80）上为较好，在[80，90）上为良好，在[90，100]上为优秀．用频率估计概率，若从参考学生中随机抽取1人，则其成绩为优良（优秀或良好）的概率为（ ）| A． | 0.09 | B． | 0.20 | C． | 0.25 | D． | 0.40 |
分析 根据题意，求出成绩在[80，100]内的频率即可．
解答 解：根据题意，成绩在[80，100]内的频率为
（0.025+0.015）×10=0.40；
所以，成绩为优良的概率为0.40．
故选：D．
点评 本题考查了用样本的频率估计总体概率的应用问题，是基础题目．
练习册系列答案
新思维寒假作业系列答案
相关题目
14．设函数f′（x）的偶函数f（x）（x∈R且x≠0）的导函数，f（2）=0且当x＞0时，xf′（x）-f（x）＞0，则使f（x）＜0成立的x的取值范围为（ ）
| A． | （-∞，-2）∪（0，2） | B． | （-2，0）∪（0，2） | C． | （-2，0）∪（2，+∞） | D． | （-∞，-2）∪（2，+∞） |
12．学校开设美术、舞蹈、计算机三门选修课，现有四名同学参与选课，且每人限选一门课程，那么不同的选课方法的种数是（ ）
| A． | 12 | B． | 24 | C． | 64 | D． | 81 |
19．（A）设函数f（x）=xcosx-sinx，x∈（0，π），则f（x）的单调性是（ ）
| A． | 增函数 | B． | 减函数 | C． | 先增后减函数 | D． | 先减后增函数 |
9．若直线2x+3y-1=0与直线4x+my+11=0平行，则它们之间的距离为（ ）
| A． | $\frac{{\sqrt{13}}}{2}$ | B． | $\frac{{2\sqrt{13}}}{13}$ | C． | $\frac{{6\sqrt{13}}}{13}$ | D． | $\frac{{12\sqrt{13}}}{13}$ |
13．与双曲线x2-$\frac{y^2}{4}$=1有共同的渐近线，且过点（2，2）的双曲线方程为（ ）
| A． | $\frac{x^2}{2}$-$\frac{y^2}{8}$=1 | B． | $\frac{x^2}{3}$-$\frac{y^2}{12}$=1 | C． | $\frac{y^2}{3}$-$\frac{x^2}{12}$=1 | D． | $\frac{y^2}{2}$-$\frac{x^2}{8}$=1 |