9.设定义在R上的奇函数f(x)在区间(0,+∞)上单调递增,则不等式f(x-1)<0的解集是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (-∞,0) |
8.假设关于某市的房屋面积x(平方米)与购房费用y(万元),有如下的统计数据
(1)用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.(假设已知y对x呈线性相关)
(2)若在该市购买120平方米的房屋,估计购房费用是多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
0 247513 247521 247527 247531 247537 247539 247543 247549 247551 247557 247563 247567 247569 247573 247579 247581 247587 247591 247593 247597 247599 247603 247605 247607 247608 247609 247611 247612 247613 247615 247617 247621 247623 247627 247629 247633 247639 247641 247647 247651 247653 247657 247663 247669 247671 247677 247681 247683 247689 247693 247699 247707 266669
| x(平方米) | 80 | 90 | 100 | 110 |
| y(万元) | 42 | 46 | 53 | 59 |
(2)若在该市购买120平方米的房屋,估计购房费用是多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
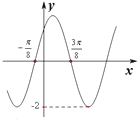 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).