Question

12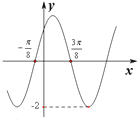．已知函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，0≤φ≤π）的部分图象如图所示，则y=f（x）的解析式是f（x）=2sin（2x+$\frac{π}{4}$）．

Answer 1

分析 由函数图象可知A的值，周期T=2（$\frac{3π}{8}+\frac{π}{8}$）=π，由周期公式可解得ω的值，由点（-$\frac{π}{8}$，0）在函数图象上，可得：2sin[2×$（-\frac{π}{8}）+$φ）]=0，结合范围0≤φ≤π，可求φ的值，即可得解．

解答 解：由函数图象可知：A=2，周期T=2（$\frac{3π}{8}+\frac{π}{8}$）=π，由周期公式可得：$ω=\frac{2π}{T}=\frac{2π}{π}=2$，
由点（-$\frac{π}{8}$，0）在函数图象上，可得：2sin[2×$（-\frac{π}{8}）+$φ）]=0，解得：φ=k$π+\frac{π}{4}$，k∈Z，
又0≤φ≤π，
从而可得：φ=$\frac{π}{4}$，
可得：$f（x）=2sin（2x+\frac{π}{4}）$，
故答案为：2sin（2x+$\frac{π}{4}$）．

点评 本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，正弦函数的图象和性质，属于基本知识的考查．