题目内容
17.已知a是实数,函数f(x)=2ax2+2x-3在x∈[-1,1]上恒小于零,求实数a的取值范围.分析 通过讨论a的值,判断函数是一次函数还是二次函数,分别根据一次函数、二次函数的性质求出a的范围即可.
解答 解:①a=0时,函数f(x)=2x-3是增函数,
而f(1)=-1<0,
∴函数f(x)=2ax2+2x-3在x∈[-1,1]上恒小于零;
②a≠0时,函数f(x)是二次函数,
若函数f(x)=2ax2+2x-3在x∈[-1,1]上恒小于零,
则只需$\left\{\begin{array}{l}{a>0}\\{△=4+24a>0}\\{{x}_{1}=\frac{-1-\sqrt{1+6a}}{2a}<-1}\\{{x}_{2}=\frac{-1+\sqrt{1+6a}}{2a}>1}\end{array}\right.$,解得:0<a<$\frac{1}{2}$
或$\left\{\begin{array}{l}{a<0}\\{△<0}\end{array}\right.$,解得:a<-1$\frac{1}{6}$,
或$\left\{\begin{array}{l}{a<0}\\{△>0}\\{{x}_{2}>1}\end{array}\right.$,解得:-$\frac{1}{6}$<a<0,
或$\left\{\begin{array}{l}{a<0}\\{△>0}\\{{x}_{1}<-1}\end{array}\right.$无解,
综上:a<$\frac{1}{2}$.
点评 本题考查了二次函数的性质,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
2.设全集U=R,集合A={x|x≥2},B={x|x≥2},B={x|0≤x<5},则集合(∁UA)∩B=( )
| A. | {x|0<x<2} | B. | {x|0<x≤2} | C. | {x|0≤x≤2} | D. | {x|0≤x<2} |
8.在△ABC中,边 a,b,c的对应角分别为A,B,C.若a=1,b=$\sqrt{3},A={30°}$,则B等于( )
| A. | 60° | B. | 60°或120° | C. | 30°或150° | D. | 120° |
6.函数f(x)=3x2-x3在下列区间上单调递增的是( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (-∞,1) | D. | (0,1) |
7.已知i是虚数单位,若$\frac{3+i}{z}=1-i$,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
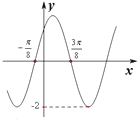 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).