3.设函数f(x)=ex(sinx-cosx)(0≤x≤2015π),则函数f(x)的各极小值之和为( )
| A. | -$\frac{{e}^{2π}(1-{e}^{2015π})}{1-{e}^{2π}}$ | B. | -$\frac{{e}^{2π}(1-{e}^{2015π)}}{1-{e}^{π}}$ | ||
| C. | -$\frac{1-{e}^{2016π}}{1-{e}^{2π}}$ | D. | -$\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$ |
2.在△ABC中,角A、B、C的对边分别为a,b,c,且满足$\sqrt{2}$acosB=bcosC+ccosB,则角B的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
1.将函数y=cos(x-$\frac{π}{3}$)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变),再向右平移$\frac{π}{6}$个单位,所得函数图象的一个对称中心为( )
| A. | $({\frac{7π}{12},0})$ | B. | $({\frac{π}{3},0})$ | C. | $({\frac{11π}{6},0})$ | D. | $({\frac{3π}{2},0})$ |
20.命题“?x∈R,sin2x>1”的否定是( )
| A. | ?x∈R,sin2x≤1 | B. | ?x∉R,sin2x>1 | C. | ?x0∈R,sin2x≤1 | D. | ?x0∉R,sin2x>1 |
16.已知函数f(x)=$\left\{\begin{array}{l}|x+1|,-7≤x≤0\\ 1nx,{e^{-2}}≤x≤e\end{array}$,g(x)=x2-2x,设a为实数,若存在实数m,使f(m)-2g(a)=0,则实数a的取值范围为( )
| A. | [-1,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,3] |
15.已知直线m,l,平面α,β,且m⊥α,l?β,给出下列命题:①若α∥β,则m⊥l; ②若α⊥β,则m∥l; ③若m⊥l,则α⊥β; ④若m∥l,则α⊥β.其中正确的命题的是( )
0 246960 246968 246974 246978 246984 246986 246990 246996 246998 247004 247010 247014 247016 247020 247026 247028 247034 247038 247040 247044 247046 247050 247052 247054 247055 247056 247058 247059 247060 247062 247064 247068 247070 247074 247076 247080 247086 247088 247094 247098 247100 247104 247110 247116 247118 247124 247128 247130 247136 247140 247146 247154 266669
| A. | ①② | B. | ③④ | C. | ①④ | D. | ①③ |
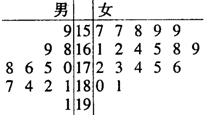 2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.
2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.