题目内容
2．在△ABC中，角A、B、C的对边分别为a，b，c，且满足$\sqrt{2}$acosB=bcosC+ccosB，则角B的大小为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
分析 由条件利用诱导公式、正弦定理，求得cosB的值，可得B的值．
解答 解：在△ABC中，由$\sqrt{2}$acosB=bcosC+ccosB利用正弦定理可得$\sqrt{2}$sinAcosB=sinBcosC+cosBsinC，
即$\sqrt{2}$sinAcosB=sin（B+C），求得cosB=$\frac{\sqrt{2}}{2}$，∴B=$\frac{π}{4}$，
故选：B．
点评 本题主要考查诱导公式、正弦定理的应用，属于基础题．
练习册系列答案
相关题目
10．在△ABC中，C=60°，AB=$\sqrt{3}$，AB边上的高为$\frac{4}{3}$，则AC+BC等于（ ）
| A． | $\sqrt{10}$ | B． | 5 | C． | 3 | D． | $\sqrt{11}$ |
如图，在四边形ABCD中，AB⊥BC，AB=3，BC=4，△ACD是等边三角形，则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$．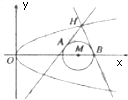
如图，已知⊙M：（x-4）2+y2=1和抛物线C：y2=2px（p＞0，其焦点为F），且$\overrightarrow{FM}$=（$\frac{15}{4}$，0，），过抛物线C上一点H（x0，y0）（y0≥1）作两条直线分别与⊙M相切于A、B两点．