��Ŀ����
19��������f��x���ڶ������ij������������f��x��=$\frac{1}{��}f��{x-��}��$����Ϊ��ʵ�����������Ϊ��-�ֲ�����������������f��x����x��[0��2]ʱ��f��x��=sin��x����x�ʣ�2��+�ޣ�ʱ��f��x��Ϊ��=2�ľֲ�������������������4�����⣺����ȡx1��x2��[0��+�ޣ�������|f��x1��-f��x2��|��2�������
��f��x��=2kf��x+2k����k��N*��������һ��x��[0��+�ޣ���������ۺ���y=f��x��-ln��x-1����5����㣻�ܶ�����x��0��������ʽf��x����$\frac{k}{x}$���������k����Сֵ��$\frac{5}{4}$��
���������������������Ǣ٢ܣ�
���� ����f��x��=$\stackrel{\left\{\begin{array}{l}{sin��x��}&{x��[0��2]}\\{\frac{1}{2}f��x-2��}&{x�ʣ�2��+�ޣ�}\end{array}\right.}{\;}$��ͼ������ͼ��ɵý��ۣ�
��� 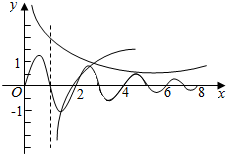 �⣺f��x��=$\stackrel{\left\{\begin{array}{l}{sin��x��}&{x��[0��2]}\\{\frac{1}{2}f��x-2��}&{x�ʣ�2��+�ޣ�}\end{array}\right.}{\;}$��ͼ����ͼ��ʾ��
�⣺f��x��=$\stackrel{\left\{\begin{array}{l}{sin��x��}&{x��[0��2]}\\{\frac{1}{2}f��x-2��}&{x�ʣ�2��+�ޣ�}\end{array}\right.}{\;}$��ͼ����ͼ��ʾ��
��f��x�������ֵΪ1����СֵΪ-1������ȡx1��x2��[0��+�ޣ�������|f��x1��-f��x2��|��2���������ȷ��
��f��$\frac{1}{2}$��=2f��$\frac{1}{2}$+2��=4f��$\frac{1}{2}$+4��=8f��$\frac{1}{2}$+6����8f��$\frac{1}{2}$+8�����ʲ���ȷ��
����ͼ��ʾ������y=f��x��-ln��x-1����3����㣻�۴���
�ܰѣ�$\frac{5}{2}$��$\frac{1}{2}$�����룬�ɵ�k��$\frac{5}{4}$����ȷ��
�ʴ�Ϊ���٢ܣ�
���� ���⿼��ֶκ�����Ӧ�ã��������ν�ϵ���ѧ˼�룬��ȷ����������ͼ���ǹؼ��������е���

��ϰ��ϵ�д�
�����Ŀ
9��������x��y����Լ������$\left\{\begin{array}{l}{x��1}\\{x+y-4��0}\\{x-y��0}\end{array}\right.$����$\frac{y}{x}$�����ֵΪ��������
| A�� | 2 | B�� | 3 | C�� | $\frac{4}{3}$ | D�� | 5 |
7����֪F��������C��y2=4x�Ľ��㣬����F��ֱ�߽�������C��A��B���㣬��|AB|=6������AB�е�ĺ�����Ϊ��������
| A�� | 1 | B�� | 2 | C�� | 4 | D�� | ��ȷ�� |
1����֪����f��x��=$\frac{1}{2}$x2+2ax��g��x��=3a2lnx+b����������y=f��x����y=g��x���й����㣬���ڸõ㴦��������ͬ����a�ʣ�0��+�ޣ�ʱ��ʵ��b�����ֵ�ǣ�������
| A�� | $\frac{3}{2}$e${\;}^{\frac{2}{3}}$ | B�� | $\frac{13}{6}$e6 | C�� | $\frac{1}{6}$e6 | D�� | $\frac{7}{2}$e${\;}^{\frac{2}{3}}$ |
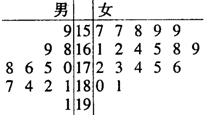 2013��8��28��-30�գ�������ԥ�̴���ڡ�����֮Դ������֮�����������о��У�Ϊ�˸�ýӴ������������ί����ijѧԺ��ļ��12����־Ը�ߺ�18��Ů־Ը�ߣ�����30��־Ը�ߵ����߱������ʾ�ľ�Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���߸��ӡ���������175cm���£�������175cm������Ϊ���Ǹ߸��ӡ�����ֻ�С�Ů�߸��ӡ��ŵ��Ρ�����С�㡱��
2013��8��28��-30�գ�������ԥ�̴���ڡ�����֮Դ������֮�����������о��У�Ϊ�˸�ýӴ������������ί����ijѧԺ��ļ��12����־Ը�ߺ�18��Ů־Ը�ߣ�����30��־Ը�ߵ����߱������ʾ�ľ�Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���߸��ӡ���������175cm���£�������175cm������Ϊ���Ǹ߸��ӡ�����ֻ�С�Ů�߸��ӡ��ŵ��Ρ�����С�㡱��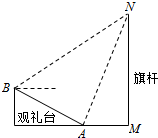 2014���������籭���Ͼ���������ʽ����ͼ�����¶�Ϊ15��Ĺ���̨�ϣ�ijһ����λ����ֱ��AB���������ֱ��MN���棬�ڸ��еĵ�һ����λA�����һ����λB�����˶���N�����Ƿֱ�Ϊ60���45�㣬����˵ĸ߶�Ϊ30�ף�������λA��B�ľ���Ϊ10��$\sqrt{6}$-$\sqrt{2}$�� �ף�
2014���������籭���Ͼ���������ʽ����ͼ�����¶�Ϊ15��Ĺ���̨�ϣ�ijһ����λ����ֱ��AB���������ֱ��MN���棬�ڸ��еĵ�һ����λA�����һ����λB�����˶���N�����Ƿֱ�Ϊ60���45�㣬����˵ĸ߶�Ϊ30�ף�������λA��B�ľ���Ϊ10��$\sqrt{6}$-$\sqrt{2}$�� �ף�