题目内容
3.设函数f(x)=ex(sinx-cosx)(0≤x≤2015π),则函数f(x)的各极小值之和为( )| A. | -$\frac{{e}^{2π}(1-{e}^{2015π})}{1-{e}^{2π}}$ | B. | -$\frac{{e}^{2π}(1-{e}^{2015π)}}{1-{e}^{π}}$ | ||
| C. | -$\frac{1-{e}^{2016π}}{1-{e}^{2π}}$ | D. | -$\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$ |
分析 先求出其导函数,利用导函数求出其单调区间,进而找到其极小值f(2kπ+2π)=e2kπ+2π,再利用数列的求和方法来求函数f(x)的各极小值之和即可.
解答 解:∵函数f(x)=ex(sinx-cosx),
∴f′(x)=(ex)′(sinx-cosx)+ex(sinx-cosx)′
=2exsinx,
∵x∈(2kπ+π,2kπ+2π)时,f′(x)<0,x∈(2kπ+2π,2kπ+3π)时,f′(x)>0,
∴x∈(2kπ+π,2kπ+2π)时原函数递减,x∈(2kπ+2π,2kπ+3π)时,函数f(x)=ex(sinx-cosx)递增,
故当x=2kπ+2π时,f(x)取极小值,
其极小值为f(2kπ+2π)=e2kπ+2π[sin(2kπ+2π)-cos(2kπ+2π)]
=e2kπ+2π×(0-1)
=-e2kπ+2π,
又0≤x≤2015π,
∴e2014π函数f(x)的各极小值之和S=-e2π-e4π-e6π-…-e2012π-e2014π
=$\frac{-{e}^{2π}[1-{(e}^{2π})^{1007}]}{1-{e}^{2π}}=-\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$
故选:D
点评 本题主要考查利用导数研究函数的极值以及等比数列的求和.利用导数求得当x=2kπ+2π时,f(x)取极小值是解题的关键,利用导数研究函数的单调性与最值是教学中的重点和难点,学生应熟练掌握,属于难题.

练习册系列答案
相关题目
4.若a是f(x)=sinx-xcosx在x∈(0,2π)的一个零点,则?x∈(0,2π),下列不等式恒成立的是( )
| A. | $\frac{sinx}{x}≥\frac{sina}{a}$ | B. | cosa≥$\frac{sinx}{x}$ | C. | $\frac{3π}{2}$≤a≤2π | D. | a-cosa≥x-cosx |
 已知椭圆C中心在坐标原点,对称轴为坐标轴,且过点A(2$\sqrt{6}$,2)、B(3,3).
已知椭圆C中心在坐标原点,对称轴为坐标轴,且过点A(2$\sqrt{6}$,2)、B(3,3).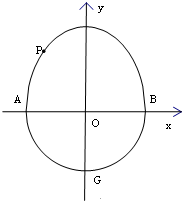 半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0,如图所示,曲线C交x轴于A,B两点,交y轴负半轴于点G.椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$的离心率为$\frac{{\sqrt{2}}}{2}$,F是它的一个焦点,点P是曲线C位于x轴上方的任意一点,且△PFG的周长是$2\sqrt{2}+2$.
半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0,如图所示,曲线C交x轴于A,B两点,交y轴负半轴于点G.椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$的离心率为$\frac{{\sqrt{2}}}{2}$,F是它的一个焦点,点P是曲线C位于x轴上方的任意一点,且△PFG的周长是$2\sqrt{2}+2$.