题目内容
18.直线l的方程为y=x+2,在l上任取一点P,若过点P且以双曲线12x2-4y2=3的焦点为椭圆的焦点作椭圆,那么具有最短长轴的椭圆方程为$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$.分析 设出椭圆方程,P的坐标,使椭圆与直线相切.由此入手能够求出具有最短长轴的椭圆方程
解答 解:设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)
c=1,a2-b2=c2=1
设P的坐标为:﹙m,m+2﹚P在椭圆上
∴$\frac{{m}^{2}}{{a}^{2}}+\frac{(m+2)^{2}}{{a}^{2}-1}$=1,
∴﹙a2-1﹚m2+a2﹙m2+4m+4﹚=a2﹙a2-1﹚=﹙a2﹚2-a2
﹙2a2-1﹚m2+4a2m+5a2-﹙a2﹚2=0
△=﹙4a2﹚2-﹙8a2-4﹚﹙5a2-a4﹚≥0
∴2a4-11a2+5≥0
∴﹙2a2-1﹚﹙a2-5﹚≥0
∴a2≤$\frac{1}{2}$或a2≥5
∵c2=1,a2>c2
∴a2≥5,长轴最短,即a2=5
b2=a2-1=4
所以:所求椭圆方程为$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$.
故答案为:$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$.
点评 本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细求解.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
8.设m,n为空间两条不同的直线,α,β为空间两个不同的平面,给出下列命题:
①若m∥α,m∥β,则α∥β;
②若m∥α,m∥n则n∥α;
③若m⊥α,m∥β,则α⊥β;
④若m⊥α,α∥β,则m⊥β.
其中的正确命题序号是( )
①若m∥α,m∥β,则α∥β;
②若m∥α,m∥n则n∥α;
③若m⊥α,m∥β,则α⊥β;
④若m⊥α,α∥β,则m⊥β.
其中的正确命题序号是( )
| A. | ③④ | B. | ②④ | C. | ①② | D. | ①③ |
6.已知函数f(x)满足条件:?x∈R,f(x)+f(-x)=0且f(x+t)-f(x)<0(其中t为正数),则函数f(x)的解析式可以是( )
| A. | y=$\frac{1}{x}$ | B. | y=x3 | C. | y=sinx | D. | y=-3x |
3.设函数f(x)=ex(sinx-cosx)(0≤x≤2015π),则函数f(x)的各极小值之和为( )
| A. | -$\frac{{e}^{2π}(1-{e}^{2015π})}{1-{e}^{2π}}$ | B. | -$\frac{{e}^{2π}(1-{e}^{2015π)}}{1-{e}^{π}}$ | ||
| C. | -$\frac{1-{e}^{2016π}}{1-{e}^{2π}}$ | D. | -$\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$ |
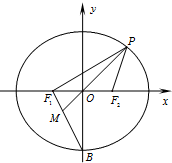 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{5}}{5}$,短轴长为4,F1、F2为椭圆左、右焦点,点B为下顶点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{5}}{5}$,短轴长为4,F1、F2为椭圆左、右焦点,点B为下顶点.