题目内容
1.将函数y=cos(x-$\frac{π}{3}$)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变),再向右平移$\frac{π}{6}$个单位,所得函数图象的一个对称中心为( )| A. | $({\frac{7π}{12},0})$ | B. | $({\frac{π}{3},0})$ | C. | $({\frac{11π}{6},0})$ | D. | $({\frac{3π}{2},0})$ |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,可得结论.
解答 解:将函数y=cos(x-$\frac{π}{3}$)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变),
可得函数y=cos(2x-$\frac{π}{3}$)的图象;
再向右平移$\frac{π}{6}$个单位,可得函数数y=cos[2(x-$\frac{π}{6}$)-$\frac{π}{3}$]=cos(2x-$\frac{2π}{3}$)图象,
故所得图象的对称中心的横坐标满足2x-$\frac{2π}{3}$=kπ+$\frac{π}{2}$,k∈z,即x=$\frac{kπ}{2}$+$\frac{7π}{12}$,k∈z,
故所得图象的对称中心为(x=$\frac{kπ}{2}$+$\frac{7π}{12}$,0)k∈z.
结合所给的选项,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
12.如表是对与喜欢足球与否的统计列联表依据表中的数据,得到( )
| 喜欢足球 | 不喜欢足球 | 总计 | |
| 男 | 40 | 28 | 68 |
| 女 | 5 | 12 | 17 |
| 总计 | 45 | 40 | 85 |
| A. | K2=9.564 | B. | K2=3.564 | C. | K2<2.706 | D. | K2>3.841 |
16.已知函数f(x)=$\left\{\begin{array}{l}|x+1|,-7≤x≤0\\ 1nx,{e^{-2}}≤x≤e\end{array}$,g(x)=x2-2x,设a为实数,若存在实数m,使f(m)-2g(a)=0,则实数a的取值范围为( )
| A. | [-1,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,3] |
 如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,
如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,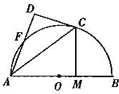 如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:
如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证: