3．数列{an}满足a1=1，a2=$\frac{1}{2}$，并且an（an-1+an+1）=2an+1an-1（n≥2），则该数列的第2015项为（ ）
| A． | $\frac{1}{2014}$ | B． | $\frac{1}{{2}^{2014}}$ | C． | $\frac{1}{2015}$ | D． | $\frac{1}{{2}^{2015}}$ |
2．大量统计数据表明，某班一周内（周一到周五）各天语文、数学、外语三科有作业的概率如下表：
根据上表：
（Ⅰ）求周五没有语文、数学、外语三科作业的概率；
（Ⅱ）设一周内有数学作业的天数为ξ，求随机变量ξ的分布列和数学期望．
| 周一 | 周二 | 周三 | 周四 | 周五 | |
| 语文 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 数学 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 外语 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
（Ⅰ）求周五没有语文、数学、外语三科作业的概率；
（Ⅱ）设一周内有数学作业的天数为ξ，求随机变量ξ的分布列和数学期望．
20．在△ABC中，E、F分别为AB、AC上的点，且AE：EB=AF：FC=1：2，P为EF上任一点，实数x、y满足$\overrightarrow{PA}$+x$\overrightarrow{PB}$+y$\overrightarrow{PC}$=$\overrightarrow{0}$，设△ABC、△PBC、△PCA、△PAB的面积分别为S、S1、S2、S3，记$\frac{{S}_{1}}{S}$=λ1，$\frac{{S}_{2}}{S}$=λ2，$\frac{{S}_{3}}{S}$=λ3，则当λ2•λ3取最大值时，2x+y的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | 1 | D． | $\frac{3}{2}$ |
18．
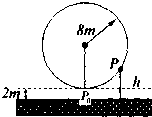一个大风车的半径为8m，12min旋转一周，它的最低点P0离地面2m，风车翼片的一个端点P从P0开始按逆时针方向旋转，则点P离地面距离h（m）与时间f（min）之间的函数关系式是（ ）
0 246882 246890 246896 246900 246906 246908 246912 246918 246920 246926 246932 246936 246938 246942 246948 246950 246956 246960 246962 246966 246968 246972 246974 246976 246977 246978 246980 246981 246982 246984 246986 246990 246992 246996 246998 247002 247008 247010 247016 247020 247022 247026 247032 247038 247040 247046 247050 247052 247058 247062 247068 247076 266669
一个大风车的半径为8m，12min旋转一周，它的最低点P0离地面2m，风车翼片的一个端点P从P0开始按逆时针方向旋转，则点P离地面距离h（m）与时间f（min）之间的函数关系式是（ ）| A． | h（t）=-8sin$\frac{π}{6}$t+10 | B． | h（t）=-cos$\frac{π}{6}$t+10 | C． | h（t）=-8sin$\frac{π}{6}$t+8 | D． | h（t）=-8cos$\frac{π}{6}$t+10 |