题目内容
7.在平面直角坐标系中,实数x,y满足$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ x-y+1≥0\end{array}\right.$,若z=-2x+y,则z的取值范围是[-2,1].分析 由约束条件作出可行域,结合图形得到使目标函数z=-2x+y的最优解,代入坐标求得z=-2x+y的最值即可.
解答 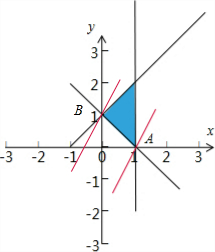 解:由约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ x-y+1≥0\end{array}\right.$作可行域如图,
解:由约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ x-y+1≥0\end{array}\right.$作可行域如图,
由图可知,可行域中点A的坐标是使目标函数z=-2x+y取得最小值的最优解.
在$\left\{\begin{array}{l}x+y-1=0\\ x-1=0\end{array}\right.$中,解得y=0得x=1.
∴点A的坐标为(1,0).
则z=-2x+y的最小值是-2×1+0=-2.
可行域中点B的坐标是使目标函数z=-2x+y取得最小值的最优解.
在$\left\{\begin{array}{l}x+y-1=0\\ x-y+1=0\end{array}\right.$中,解得y=1得x=0.
∴点B的坐标为(0,1).
则z=-2x+y的最小值是-2×0+1=1.
z的取值范围是:[-2,1].
故答案为:[-2,1]
点评 本题考查了简单的线性规划,体现了数形结合的解题思想方法,解答的关键是正确作出可行域,是中档题.

练习册系列答案
相关题目
2.大量统计数据表明,某班一周内(周一到周五)各天语文、数学、外语三科有作业的概率如下表:
根据上表:
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
| 周一 | 周二 | 周三 | 周四 | 周五 | |
| 语文 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 数学 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 外语 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
12.已知数列{an}为递增等比数列,其前n项和为Sn.若a1=1,2an+1+2an-1=5an(n≥2),则S5=( )
| A. | $\frac{31}{16}$ | B. | $\frac{31}{32}$ | C. | 31 | D. | 15 |
19.某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( ) 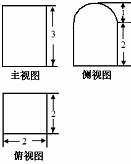

| A. | 20+2π | B. | 20+3π | C. | 24+3π | D. | 24+3π |
17.等差数列{an}中,若a4+a8=-3,则a6(a2+2a6+a10)的值是( )
| A. | -9 | B. | 9 | C. | -6 | D. | 3 |
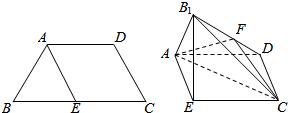 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.