题目内容
5.三棱锥S-ABC及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为4$\sqrt{2}$.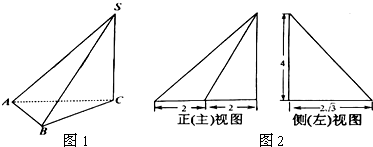
分析 由已知中的三视图可得SC⊥平面ABC,底面△ABC为等腰三角形,SC=4,△ABC中AC=4,AC边上的高为2$\sqrt{3}$,进而根据勾股定理得到答案.
解答 解:由已知中的三视图可得SC⊥平面ABC,
且底面△ABC为等腰三角形,
在△ABC中AC=4,AC边上的高为2$\sqrt{3}$,
故BC=4,
在Rt△SBC中,由SC=4,
可得SB=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$
点评 本题考查的知识点是简单空间图象的三视图,其中根据已知中的视图分析出几何体的形状及棱长是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在△ABC中,E、F分别为AB、AC上的点,且AE:EB=AF:FC=1:2,P为EF上任一点,实数x、y满足$\overrightarrow{PA}$+x$\overrightarrow{PB}$+y$\overrightarrow{PC}$=$\overrightarrow{0}$,设△ABC、△PBC、△PCA、△PAB的面积分别为S、S1、S2、S3,记$\frac{{S}_{1}}{S}$=λ1,$\frac{{S}_{2}}{S}$=λ2,$\frac{{S}_{3}}{S}$=λ3,则当λ2•λ3取最大值时,2x+y的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{3}{2}$ |
17.对于定义在R上的函数f(x),若存在x0使得$\underset{\underbrace{f(f…(f({x}_{0})))}}{k}$=x0(*),其中k为某个正整数,则称x0为函数f(x)的一个周期点,使得(*)式成立的正整数k称为x0的周期,使得(*)式成立的最小正整数k称为x0的最小周期,若函数f(x)=1-|2x-1|,则函数f(x)( )
| A. | 恰有一个最小周期为1的周期点,恰有一个最小周期为2的周期点 | |
| B. | 恰有一个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| C. | 恰有两个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| D. | 恰有两个最小周期为1的周期点,恰有四个最小周期为2的周期点 |
15.点P在直径为5的球面上,过P作两两互相垂直的三条弦(两端点均在球面上的线段),若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
| A. | 2$\sqrt{14}$ | B. | 2$\sqrt{70}$ | C. | $\sqrt{70}$ | D. | $\sqrt{14}$ |
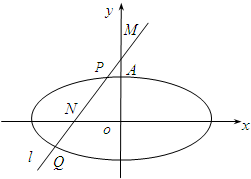 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.