题目内容
20.在△ABC中,E、F分别为AB、AC上的点,且AE:EB=AF:FC=1:2,P为EF上任一点,实数x、y满足$\overrightarrow{PA}$+x$\overrightarrow{PB}$+y$\overrightarrow{PC}$=$\overrightarrow{0}$,设△ABC、△PBC、△PCA、△PAB的面积分别为S、S1、S2、S3,记$\frac{{S}_{1}}{S}$=λ1,$\frac{{S}_{2}}{S}$=λ2,$\frac{{S}_{3}}{S}$=λ3,则当λ2•λ3取最大值时,2x+y的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{3}{2}$ |
分析 由题意可得EF平行且等于$\frac{1}{3}$BC,可得 λ1=$\frac{2}{3}$,λ2+λ3=$\frac{1}{3}$,利用基本不等式求得λ2•λ3取得组大值时λ2=λ3=$\frac{1}{6}$,且P为EF的中点,$\overrightarrow{PA}$=-$\frac{1}{4}$($\overrightarrow{PB}$+$\overrightarrow{PC}$ ).由已知$\overrightarrow{PA}$=-x$\overrightarrow{PB}$+(-y)$\overrightarrow{PC}$,求得x和y的值,可得2x+y的值.
解答 解:∵△ABC、△PBC、△PCA、△PAB的面积分别为S、S1、S2、S3,
$\frac{{S}_{1}}{S}$=λ1,$\frac{{S}_{2}}{S}$=λ2,$\frac{{S}_{3}}{S}$=λ3,∴λ1+λ2+λ3=1.
∵E、F分别为AB、AC上的点,且AE:EB=AF:FC=1:2,可得E、F分别为 AB、AC的一个三等分点,
且EF平行且等于$\frac{1}{3}$BC,
P为EF上任一点,∴λ1=$\frac{{S}_{1}}{S}$=$\frac{\frac{1}{2}•BC•\frac{2}{3}h}{\frac{1}{2}•BC•h}$=$\frac{2}{3}$,∴λ2+λ3=$\frac{1}{3}$≥2$\sqrt{{λ}_{2}{•λ}_{3}}$,
∴λ2•λ3≤$\frac{1}{36}$,当且仅当λ2=λ3=$\frac{1}{6}$时,取等号,此时,P为EF的中点,
$\overrightarrow{PA}$=-$\frac{1}{2}$•[$\frac{1}{2}$($\overrightarrow{PB}$+$\overrightarrow{PC}$ )]=-$\frac{1}{4}$($\overrightarrow{PB}$+$\overrightarrow{PC}$ ).
由已知$\overrightarrow{PA}$+x$\overrightarrow{PB}$+y$\overrightarrow{PC}$=$\overrightarrow{0}$,可得$\overrightarrow{PA}$=-x$\overrightarrow{PB}$+(-y)$\overrightarrow{PC}$,故有x=$\frac{1}{4}$,y=$\frac{1}{4}$,∴2x+y=$\frac{3}{4}$,
故选:B.
点评 本题考查向量在几何中的应用,综合性强,难度大,是高考的重点,计算繁琐,容易出错.解题时要认真审题,仔细解答,注意转化思想的合理运用,属于中档题.

| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
| A. | f(2a)<f(3)<f(log2a) | B. | f(3)<f(log2a)<f(2a) | C. | f(log2a)<f(3)<f(2a) | D. | f(log2a)<f(2a)<f(3) |
| A. | $\frac{31}{16}$ | B. | $\frac{31}{32}$ | C. | 31 | D. | 15 |
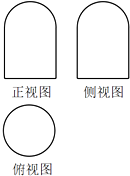 一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.
一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.