7．已知四面体ABCD的所有顶点都在球O的球面上，球O的半径为2，AB，AC，AD两两垂直，AB=$\sqrt{2}$，则四面体ABCD体积的最大值为（ ）
| A． | $\frac{7\sqrt{2}}{6}$ | B． | $\frac{7}{3}$ | C． | 2$\sqrt{2}$ | D． | 2 |
6．已知点P为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上一点，点F1，F2分别为椭圆的左、右焦点，点I为△PF1F2的内心，若△PIF1和△PIF2的面积和为1，则△IF1F2的面积为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
5．小王参加网购后，快递员电话通知于本周五早上7：30-8：30送货到家，如果小王这一天离开家的时间为早上8：00-9：00，那么在他走之前拿到邮件的概率为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{7}{8}$ |
4．
将棱长为1的正方体截去若干个角后，得到某几何体的三视图，如图所示，它们都是边长为1的正方形，则该几何体的体积为（ ）
将棱长为1的正方体截去若干个角后，得到某几何体的三视图，如图所示，它们都是边长为1的正方形，则该几何体的体积为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
3．执行如图程序框图，若输出的S值为62，则判断框内为（ ）
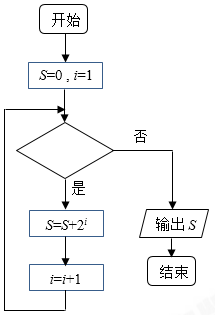
| A． | i≤4？ | B． | i≤5？ | C． | i≤6？ | D． | i≤7？ |
2．设x，y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≥2}\\{x≤2}\end{array}\right.$，则z=2x+y+1的最大值为（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
1．焦点在y轴上的双曲线的一条渐近方程为y=$\frac{\sqrt{3}}{3}$x，则双曲线的离心率为（ ）
| A． | 2 | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | $\frac{4\sqrt{3}}{3}$ |
19．设全集U={1，2，3，4，5，6，7}，P={1，2，3，4}，Q={3，4，5，6}，则P∩（∁UQ）=（ ）
0 246763 246771 246777 246781 246787 246789 246793 246799 246801 246807 246813 246817 246819 246823 246829 246831 246837 246841 246843 246847 246849 246853 246855 246857 246858 246859 246861 246862 246863 246865 246867 246871 246873 246877 246879 246883 246889 246891 246897 246901 246903 246907 246913 246919 246921 246927 246931 246933 246939 246943 246949 246957 266669
| A． | {1，2，3，4，5，6} | B． | {1，2，3，4，5} | C． | {1，2，5} | D． | {1，2} |