题目内容
4. 将棱长为1的正方体截去若干个角后,得到某几何体的三视图,如图所示,它们都是边长为1的正方形,则该几何体的体积为( )
将棱长为1的正方体截去若干个角后,得到某几何体的三视图,如图所示,它们都是边长为1的正方形,则该几何体的体积为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 由已知中的三视图可得:该几何体是棱长为1的正方体截去两个角所得的组合体,画出其直观图,并求出截去部分的体积,相减可得答案.
解答 解:由已知中的三视图可得:该几何体是棱长为1的正方体截去两个角所得的组合体,
其直观图如下图所示: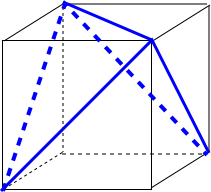
故组合体的体积V=1-2($\frac{1}{3}$×$\frac{1}{2}$×1×1×1)=$\frac{2}{3}$,
故选:C
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
12.已知圆x2+y2+x+2y=$\frac{61}{16}$和圆(x-sinα)2+(y-1)2=$\frac{1}{16}$,其中0°≤α≤90°,则两圆的位置关系是( )
| A. | 相交 | B. | 外切 | C. | 内切 | D. | 相交或内切 |
19.设全集U={1,2,3,4,5,6,7},P={1,2,3,4},Q={3,4,5,6},则P∩(∁UQ)=( )
| A. | {1,2,3,4,5,6} | B. | {1,2,3,4,5} | C. | {1,2,5} | D. | {1,2} |
9.某市教育局邀请教育专家深入该市多所中小学,开展听课,访谈及随堂检测等活动.他们把收集到的180节课分为三类课堂教学模式:教师主讲的为A模式,少数学生参与的为B模式,多数学生参与的为C模式,A、B、C三类课的节数比例为3:2:1.
(Ⅰ)为便于研究分析,教育专家将A模式称为传统课堂模式,B、C统称为新课堂模式.根据随堂检测结果,把课堂教学效率分为高效和非高效,根据检测结果统计得到如下2×2列联表(单位:节)
请根据统计数据回答:有没有99%的把握认为课堂教学效率与教学模式有关?并说明理由.
(Ⅱ)教育专家用分层抽样的方法从收集到的180节课中选出12节课作为样本进行研究,并从样本中的B模式和C模式课堂中随机抽取2节课,求至少有一节课为C模式课堂的概率.
参考临界值表:
参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$
其中n =a +b +c +d).
(Ⅰ)为便于研究分析,教育专家将A模式称为传统课堂模式,B、C统称为新课堂模式.根据随堂检测结果,把课堂教学效率分为高效和非高效,根据检测结果统计得到如下2×2列联表(单位:节)
| 高效 | 非高效 | 总计 | |
| 新课堂模式 | 60 | 30 | 90 |
| 传统课堂模式 | 40 | 50 | 90 |
| 总计 | 100 | 80 | 180 |
(Ⅱ)教育专家用分层抽样的方法从收集到的180节课中选出12节课作为样本进行研究,并从样本中的B模式和C模式课堂中随机抽取2节课,求至少有一节课为C模式课堂的概率.
参考临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
其中n =a +b +c +d).
13.已知集合M={x|y=lg(1-x)},集合N={y|y=2x,x∈R},则M∩N=( )
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
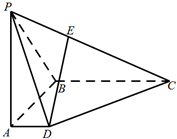 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1. 如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.
如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.