题目内容
8.已知sin$\frac{α}{8}$=-$\frac{3}{5}$,8π<α<12π,则tan$\frac{α}{4}$=$\frac{24}{7}$.分析 由已知可得π<$\frac{α}{8}$<$\frac{3π}{2}$,2π<$\frac{α}{4}$<3π,由同角三角函数关系式即可求sin$\frac{α}{8}$,cos$\frac{α}{8}$,由倍角公式即可求sin$\frac{α}{4}$,cos$\frac{α}{4}$,由同角三角函数关系式即可求得tan$\frac{α}{4}$.
解答 解:∵8π<α<12π,
∴π<$\frac{α}{8}$<$\frac{3π}{2}$,2π<$\frac{α}{4}$<3π,
∴cos$\frac{α}{8}$=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,
∴sin$\frac{α}{4}$=2sin$\frac{α}{8}$cos$\frac{α}{8}$=2×$(-\frac{3}{5})×(-\frac{4}{5})$=$\frac{24}{25}$,
∴cos$\frac{α}{4}$=2cos2$\frac{α}{8}$-1=2×$(-\frac{4}{5})^{2}-1$=$\frac{7}{25}$,
∴tan$\frac{α}{4}$=$\frac{sin\frac{α}{4}}{cos\frac{α}{4}}$=$\frac{24}{7}$.
故答案为:$\frac{24}{7}$.
点评 本题主要考查了倍角公式及同角三角函数关系式的应用,属于基本知识的考查.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
16.设F1、F2分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,双曲线上存在一点P,使得|PF1|+|PF2|=3b,|PF1|•|PF2|=$\frac{9}{4}$ab,则该双曲线的渐近线方程为( )
| A. | y=±$\frac{4}{3}$x | B. | y=±$\frac{3}{4}$x | C. | y=±$\frac{5}{3}$x | D. | y=±$\frac{3}{5}$x |
3.执行如图程序框图,若输出的S值为62,则判断框内为( )
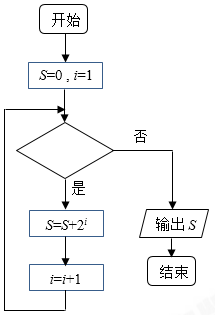

| A. | i≤4? | B. | i≤5? | C. | i≤6? | D. | i≤7? |