题目内容
5.小王参加网购后,快递员电话通知于本周五早上7:30-8:30送货到家,如果小王这一天离开家的时间为早上8:00-9:00,那么在他走之前拿到邮件的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{8}$ |
分析 设快递员到达的时间为x,小王离家去工作的时间为y,则(x,y)可以看成平面中的点,根据几何概型概率公式得到结果.
解答 解:设快递员到达的时间为x,小王离家去工作的时间为y,
则满足$\left\{\begin{array}{l}{7.5≤x≤8.5}\\{8≤y≤9}\end{array}\right.$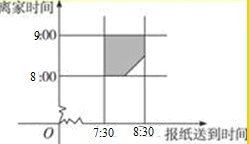
记在他走之前拿到邮件的事件A;则满足x<y,
以横坐标表示报纸送到时间,以纵坐标表示小明爸爸离家时间,建立平面直角坐标系,
则对应区域的概率P=$\frac{1-\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}{1}$=1-$\frac{1}{8}$=$\frac{7}{8}$,
故选:D
点评 本题主要考查几何概型的概率计算,对于这样的问题,一般要通过把试验发生包含的事件所对应的区域求出,根据集合对应的图形面积,用面积的比值得到结果.

练习册系列答案
相关题目
15.如图△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,则BD的长为( )


| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
13.已知i为虚数单位,复数z满足z(2-i)=10+5i,则z等于( )
| A. | 3+4i | B. | 3-4i | C. | -3+4i | D. | -3-4i |

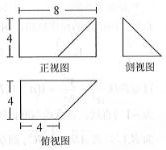 已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.
已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.