19.已知函数f(n)=logn+1(n+2)(n∈N*),定义使f(1)•f(2)…f(k)为整数的数k(k∈N*)叫做企盼数,则在区间[1,50]内这样的企盼数共有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}+1,x<1}\\{{x}^{2}+ax,x≥1}\end{array}\right.$,若f(f(0))=6,则a的值等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | 4 |
17.函数f(x)=x+lgx的零点所在的区间为( )
| A. | (0,$\frac{1}{10}$) | B. | ($\frac{1}{10}$,1) | C. | (1,10) | D. | (10,+∞) |
16.为了得到函数y=cos(2x+$\frac{π}{3}$),x∈R的图象,只需把函数y=cos2x的图象( )
| A. | 向左平行移动$\frac{π}{6}$个单位长度 | B. | 向左平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向右平行移动$\frac{π}{3}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
15.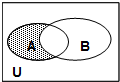 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )| A. | {x|x>1} | B. | {x|1<x≤$\frac{4}{3}$} | C. | {x|x≤1} | D. | {x|x>$\frac{4}{3}$} |
14.下列函数中,既是奇函数,又在定义域内为减函数的是( )
| A. | y=(${\frac{1}{2}}$)x | B. | y=-x2 | C. | y=-x3 | D. | y=log3(-x) |
13.某地近几年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
| 年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
| 年需求量(万吨) | 257 | 276 | 298 | 298 | 318 |
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
12.已知圆C:(x-1)2+(y-1)2=9,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)
(1)若m=0,求直线被圆C截得的弦长;
(2)证明:不论m取什么实数,直线l与圆恒交于两点.
0 246533 246541 246547 246551 246557 246559 246563 246569 246571 246577 246583 246587 246589 246593 246599 246601 246607 246611 246613 246617 246619 246623 246625 246627 246628 246629 246631 246632 246633 246635 246637 246641 246643 246647 246649 246653 246659 246661 246667 246671 246673 246677 246683 246689 246691 246697 246701 246703 246709 246713 246719 246727 266669
(1)若m=0,求直线被圆C截得的弦长;
(2)证明:不论m取什么实数,直线l与圆恒交于两点.
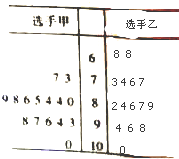 某娱乐栏目有两名选手进行最后决赛,在赛前为调查甲、乙两位选手的受欢迎程度,随机地从现场选择了15位观众对两位选手进行评分,根据评分(评分越高表明越受观众欢迎),绘制茎叶图如下:
某娱乐栏目有两名选手进行最后决赛,在赛前为调查甲、乙两位选手的受欢迎程度,随机地从现场选择了15位观众对两位选手进行评分,根据评分(评分越高表明越受观众欢迎),绘制茎叶图如下: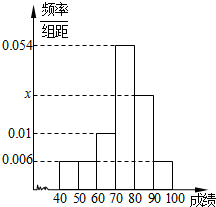 某班50位学生期中考试数学成绩的频率分布直方图如图所示.
某班50位学生期中考试数学成绩的频率分布直方图如图所示.