题目内容
13.某地近几年粮食需求量逐年上升,下表是部分统计数据:| 年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
| 年需求量(万吨) | 257 | 276 | 298 | 298 | 318 |
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
分析 (I)利用最小二乘法做出b,a,写出线性回归方程.
(II)把所给的x的值代入线性回归方程,求出变化以后的预报值,得到结果.
解答 解:由数据可得$\overline{x}$=$\frac{1}{5}$(2006+2008+2010+2012+2014)=2010,
$\overline{y}$=$\frac{1}{5}$(257+276+286+298+318)=287,
$\stackrel{∧}{b}$=$\frac{2006×257+2008×276+2010×286+2012×298+2014×318-5×2010×287}{200{6}^{2}+200{8}^{2}+201{0}^{2}+201{2}^{2}+201{4}^{2}-5×201{0}^{2}}$=$\frac{288}{40}$=7.2,
$\stackrel{∧}{a}$=$\overline{y}-$$\stackrel{∧}{b}$$•\overline{x}$=287-7.2×2010=-14185;
故回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$=7.2x-14185.
(2)∵回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$=7.2x-14185.
∴当x=2015时,$\stackrel{∧}{y}$=7.2×2015-14185=323.
故预测该地2015年的粮食需求量为323(万吨).
点评 本题考查回归分析的基本思想及其初步应用,考查回归方程的意义和求法,考查数据处理的基本方法和能力,考查利用统计思想解决实际问题的能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
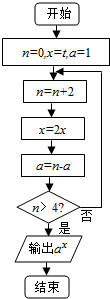
4.执行如图所示的程序框图,若结束时输出的结果不小于3,则t的取值范围为( )

| A. | [$\frac{1}{4}$,+∞) | B. | [$\frac{1}{8}$,+∞) | C. | (-∞,$\frac{1}{8}$] | D. | (-$∞,\frac{1}{4}$] |
18.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}+1,x<1}\\{{x}^{2}+ax,x≥1}\end{array}\right.$,若f(f(0))=6,则a的值等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | 4 |
5.下列函数是偶函数的是( )
| A. | y=sin2x | B. | y=lnx | C. | y=ex | D. | y=|x| |