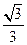题目内容
(本题满分12分)已知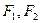 分别是椭圆
分别是椭圆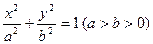 的左右焦点,其左准线与
的左右焦点,其左准线与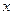 轴相交于点N,并且满足
轴相交于点N,并且满足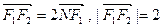 ,设A、B是上半椭圆上满足
,设A、B是上半椭圆上满足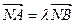 的两点,其中
的两点,其中 .(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.
.(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.
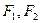 分别是椭圆
分别是椭圆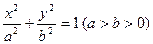 的左右焦点,其左准线与
的左右焦点,其左准线与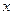 轴相交于点N,并且满足
轴相交于点N,并且满足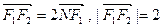 ,设A、B是上半椭圆上满足
,设A、B是上半椭圆上满足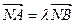 的两点,其中
的两点,其中 .(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.
.(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.(Ⅰ)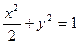 (Ⅱ)
(Ⅱ) 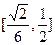
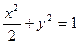 (Ⅱ)
(Ⅱ) 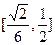
:(1)由于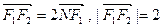 , ∴
, ∴ ,解得
,解得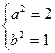 ,
,
∴椭圆的方程是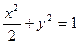 ---3分
---3分
(2)∵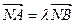 ,∴
,∴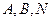 三点共线,而
三点共线,而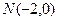 ,设直线的方程为
,设直线的方程为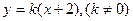 ,
,
由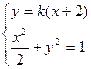 消去
消去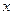 得:
得: 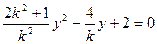
由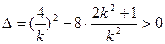 ,解得
,解得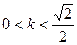 ------------6分
------------6分
设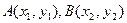 ,由韦达定理得
,由韦达定理得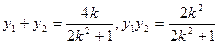 ①,
①,
又由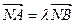 得:
得: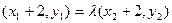 ,∴
,∴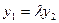 ②.
②.
将②式代入①式得: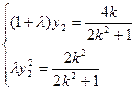 , 消去
, 消去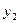 得:
得: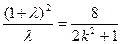 ----8分
----8分
设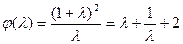 ,当
,当 时,
时,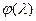 是减函数,
是减函数,
∴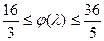 , ---10分∴
, ---10分∴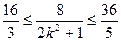 ,解得
,解得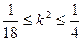 ,又由
,又由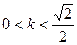 得
得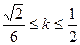 ,∴直线AB的斜率的取值范围是
,∴直线AB的斜率的取值范围是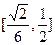 . --12分
. --12分
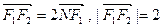 , ∴
, ∴ ,解得
,解得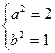 ,
,∴椭圆的方程是
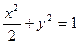 ---3分
---3分(2)∵
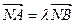 ,∴
,∴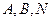 三点共线,而
三点共线,而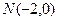 ,设直线的方程为
,设直线的方程为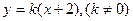 ,
,由
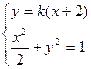 消去
消去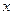 得:
得: 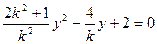
由
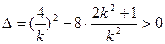 ,解得
,解得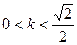 ------------6分
------------6分设
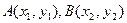 ,由韦达定理得
,由韦达定理得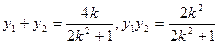 ①,
①,又由
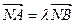 得:
得: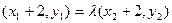 ,∴
,∴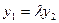 ②.
②.将②式代入①式得:
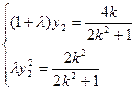 , 消去
, 消去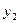 得:
得: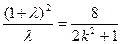 ----8分
----8分设
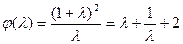 ,当
,当 时,
时,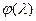 是减函数,
是减函数,∴
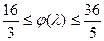 , ---10分∴
, ---10分∴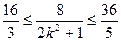 ,解得
,解得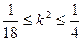 ,又由
,又由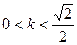 得
得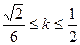 ,∴直线AB的斜率的取值范围是
,∴直线AB的斜率的取值范围是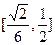 . --12分
. --12分
练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
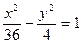
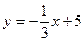 与曲线
与曲线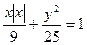 的交点个数是 ( )
的交点个数是 ( ) 0个 B
0个 B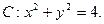
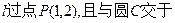 A、B两点,若
A、B两点,若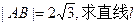 的方程;
的方程;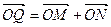 ,求动点Q的轨迹方程,并说明此轨迹是什么曲线。
,求动点Q的轨迹方程,并说明此轨迹是什么曲线。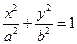
 的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点
的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点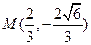 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.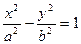 的离心率为
的离心率为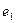 ,双曲线
,双曲线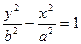 的离心率为
的离心率为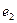 ,则
,则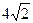
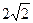
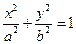
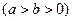 的左、右焦点分别为
的左、右焦点分别为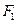 、
、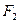 ,抛物线
,抛物线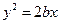 的焦点为
的焦点为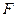 .若
.若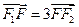 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )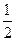 B.
B.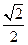 C.
C.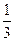 D.
D.