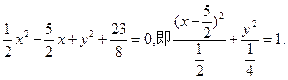题目内容
已知双曲线x2－3y2＝3的右焦点为F，右准线为l，以F为左焦点，以l为左准线的椭圆C的中心为A，又A点关于直线y＝2x的对称点A’恰好在双曲线的左准线上，求椭圆的方程．
见解析
依题意，F（2，0），l：
则
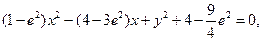
其中心为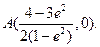
∵A与A’关于直线y＝2x对称，∴A’的坐标为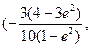
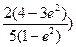
又A’在直线
。
于是所求方程为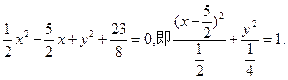
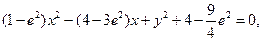
则 其中心为
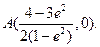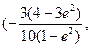
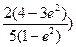
∵A与A’关于直线y＝2x对称，∴A’的坐标为又A’在直线
。于是所求方程为
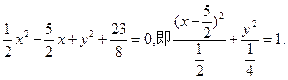
练习册系列答案
相关题目
题目内容
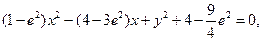
则 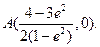∵A与A’关于直线y＝2x对称，∴A’的坐标为。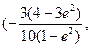
－
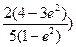
=1右支于M，N两点，A1，A2为双曲线的左右两个顶点，求直线A1M与A2N的交点P的轨迹方程，并指出轨迹的形状．
，椭圆经过点
，它们在
轴上有共同焦点，椭圆的对称轴是坐标轴．（Ⅰ）求椭圆的方程；（Ⅱ）若
是椭圆上的点，设
的坐标为
（
是已知正实数），求
，
，其焦点在
轴上，则该椭圆的标准方程为 。
是椭圆
上的一点，
,
是椭圆的两个焦点,且满足
.(Ⅰ)求椭圆的方程及离心率;(Ⅱ)设点
,
是椭圆上的两点,直线
,
的倾斜角互补,试判断直线
的斜率是否为定值?并说明理由.
分别是椭圆
的左右焦点，其左准线与
轴相交于点N，并且满足
，设A、B是上半椭圆上满足
的两点，其中
.（1）求此椭圆的方程；（2）求直线AB的斜率的取值范围.
，又抛物线
的焦点与双曲线一个焦点重合．
的方程；
是
轴上的两点，过
做直线与抛物线
两点，试证:直线
与
轴所成的锐角相等．
的斜率为1，问
的面积是否有最大值?若有，求出最大值．若没有，说明理由．