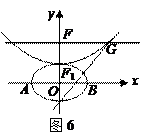题目内容
若点P到点F(
,0)的距离与它到直线x+
=0的距离相等.
(1)求P点轨迹方程C,
(2)A点是曲线C上横坐标为8且在X轴上方的点,过A点且斜率为1的直线l与C的另一个交点为B,求C与l所围成的图形的面积.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求P点轨迹方程C,
(2)A点是曲线C上横坐标为8且在X轴上方的点,过A点且斜率为1的直线l与C的另一个交点为B,求C与l所围成的图形的面积.
(1)因为点P到点F(
,0)的距离与它到直线x+
=0的距离相等
所以P点轨迹为以点F(
,0)为焦点的抛物线,
其方程为y2=2x;
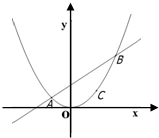
(2)当x=8时A点坐标为(8,4),故AF直线方程为
y-4=1×(x-8),即y=x-4.
作出曲线y2=2x,y=x-4的草图如图,
解方程组
,得B(2,-2)
所求面积为S=2
(
)dx+
(
-(x-4))dx
=2
x
dx+
x
dx
xdx
4dx
=
+
-
+4
=
×2
+
(8
-2
)-
(82-22)+24=18.
所以C与l所围成的图形的面积为18.
| 1 |
| 2 |
| 1 |
| 2 |
所以P点轨迹为以点F(
| 1 |
| 2 |
其方程为y2=2x;
(2)当x=8时A点坐标为(8,4),故AF直线方程为
y-4=1×(x-8),即y=x-4.
作出曲线y2=2x,y=x-4的草图如图,
解方程组
|
所求面积为S=2
| ∫ | 20 |
| 2x |
| ∫ | 82 |
| 2x |
=2
| 20 |
| 1 |
| 2 |
| 82 |
| 1 |
| 2 |
| -∫ | 82 |
| +∫ | 82 |
=
4
| ||
| 3 |
x
| 20 |
2
| ||
| 3 |
x
| 82 |
| 1 |
| 2 |
| x2| | 82 |
| x| | 82 |
=
4
| ||
| 3 |
| 3 |
| 2 |
2
| ||
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
所以C与l所围成的图形的面积为18.


练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 分别是椭圆
分别是椭圆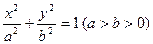 的左右焦点,其左准线与
的左右焦点,其左准线与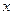 轴相交于点N,并且满足
轴相交于点N,并且满足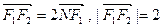 ,设A、B是上半椭圆上满足
,设A、B是上半椭圆上满足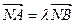 的两点,其中
的两点,其中 .(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.
.(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.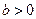 ,椭圆方程为
,椭圆方程为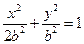 ,抛物线方程为
,抛物线方程为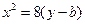 .如图6所示,过点
.如图6所示,过点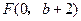 作
作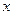 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为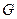 ,已知抛物线在点
,已知抛物线在点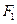 .
.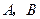 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点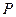 ,使得
,使得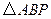 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).